5.1. Prúdový usmerňovač s induktívnou záťažou

Zapojenie na Obr. 5.1 predstavuje jednocestný prúdový usmerňovač s nulovou diódou. Dióda \(D_1\) je usmerňovacia a je vodivá počas prvého (aktívneho) intervalu, Obr. 5.2, kedy je záťaž pripojená ku zdroju (dióda \(D_2\) je nevodivá) a dochádza ku akumulácii energie do zážťaže (prúd stúpa). V okamihu zmeny polarity vstupného napätia nastáva druhý (neaktívny/nulový) interval, Obr. 5.3, kedy sa dióda \(D_1\) zatvorí (odpojenie od zdroja) a otvorí sa nulová dióda \(D_2\). V druhom intervale má prúd v obvode klesajúci charakter a trvá až do zániku prúdu, alebo do okamihu ďalšieho otvorenia diódy \(D_1\). Pre správnu činnoť meniča musíme korektne opísať všetky stavy jeho činnosti.

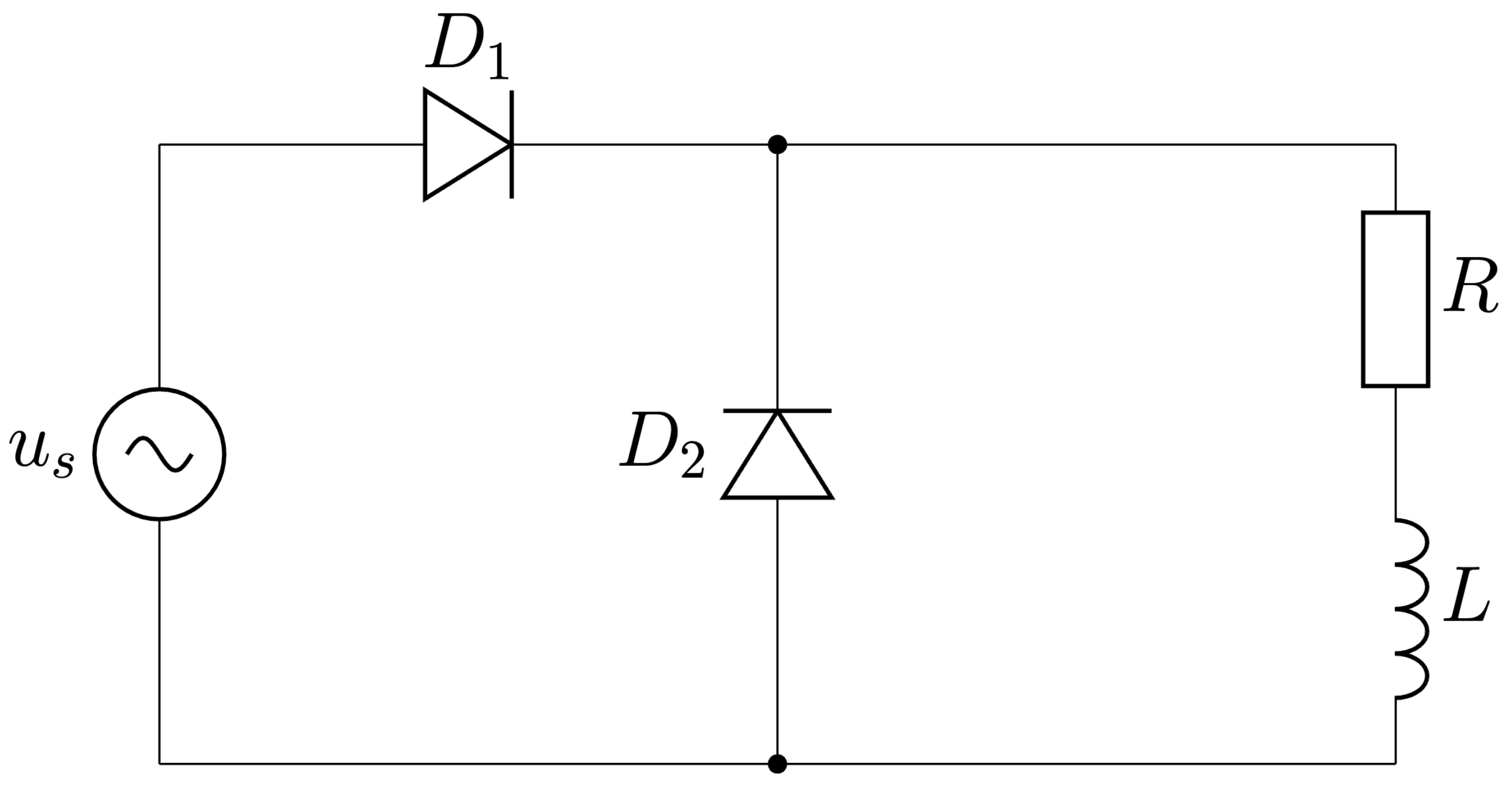
Obr. 5.1 Prúdový usmerňovač s induktívnou záťažou.

Pre analýzu aktívneho stavu tohoto meniča, Obr. 5.2, použijeme druhý Kirchhoffov zákon na získanie diferenciálnej rovnice

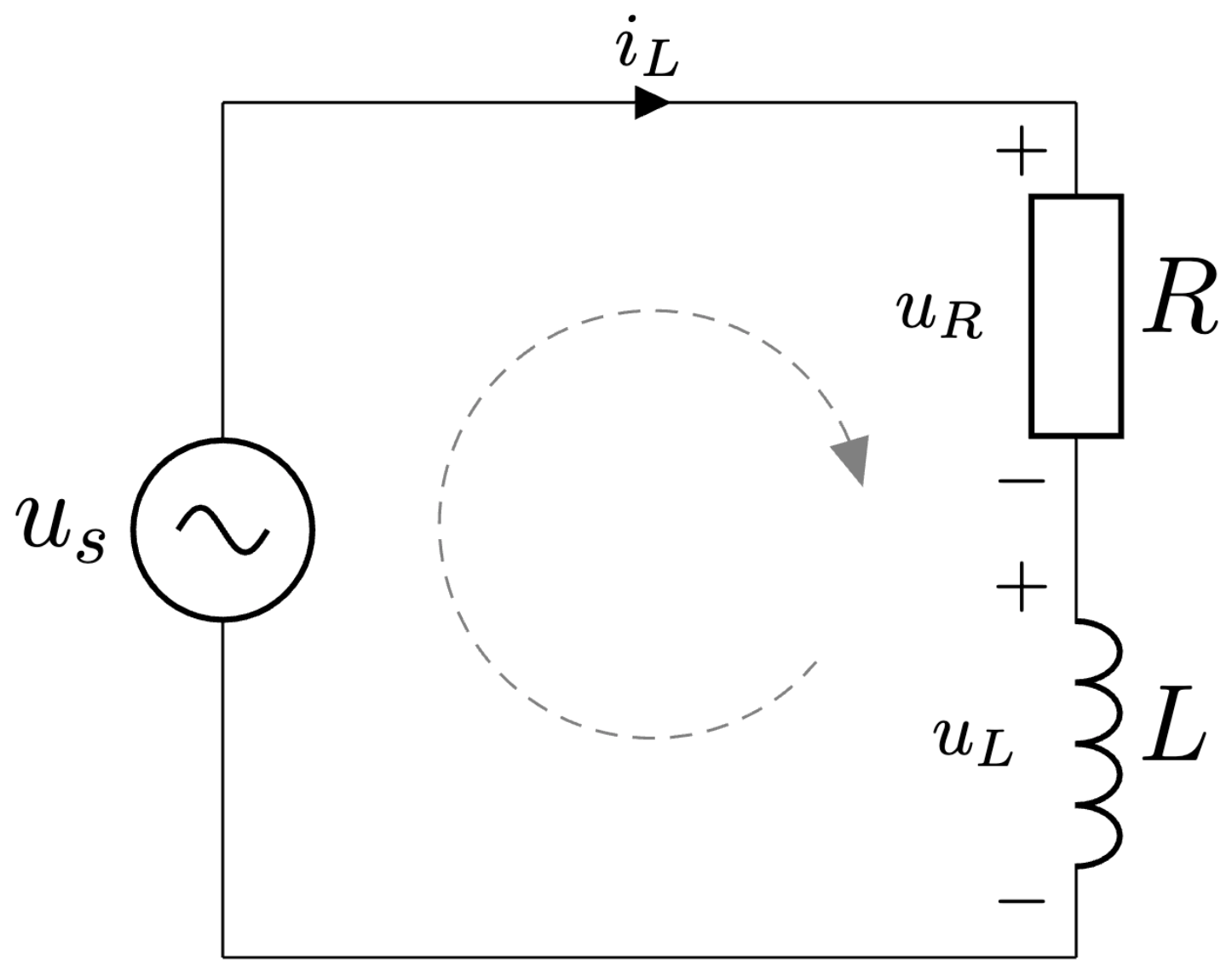
Obr. 5.2 Prúdový usmerňovač s induktívnou záťažou - aktívny interval.

(5.1)\[\begin{split} \begin{align} \begin{split} \begin{split} -u_{s} + u_L + u_R &= 0, \\ -u_{s} + L \frac{\mathrm{d} i_L}{\mathrm{d} t} + R \, i_L &= 0, \\ L \frac{\mathrm{d} i_L}{\mathrm{d} t} &= -R \, i_L + u_{s}, \\ \frac{\mathrm{d}i_L}{\mathrm{d} t} &= -\frac{R}{L}\, i_L + \frac{1}{L} u_{s}. \end{split} \end{split} \end{align} \end{split}\]

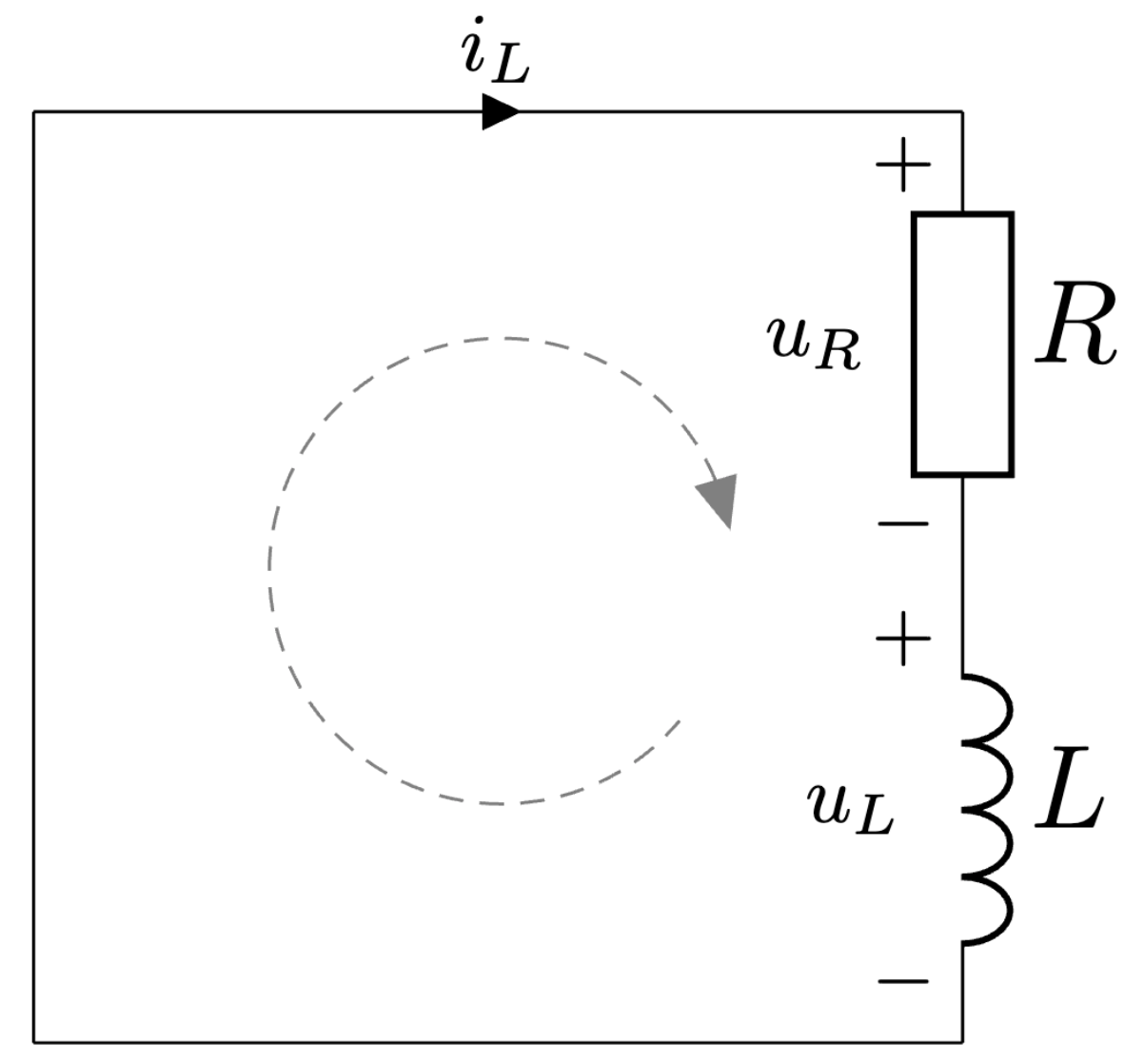
Obr. 5.3 Prúdový usmerňovač s induktívnou záťažou - nulový interval.

Pre analýzu nulového stavu tohoto meniča, Obr. 5.3, použijeme druhý Kirchhoffov zákon na získanie diferenciálnej rovnice

(5.2)\[\begin{split} \begin{align} \begin{split} \begin{split} u_L + u_R &= 0, \\ L \frac{\mathrm{d} i_L}{\mathrm{d} t} + R \, i_L &= 0, \\ L \frac{\mathrm{d} i_L}{\mathrm{d} t} &= -R \, i_L, \\ \frac{\mathrm{d} i_L}{\mathrm{d} t} &= -\frac{R}{L}\, i_L. \end{split} \end{split} \end{align} \end{split}\]

5.1.1. Stavový opis

Získali sme diferenciálnu rovnicu pre prvý stav

(5.3)\[ \begin{align} \frac{\mathrm{d} i_L}{\mathrm{d} t} &= -\frac{R}{L}\, i_L + \frac{1}{L} u_{s} \end{align} \]

a pre druhý stav

(5.4)\[ \begin{align} \frac{\mathrm{d} i_L}{\mathrm{d} t} &= -\frac{R}{L}\, i_L. \end{align} \]

Z týchto rovníc vytvoríme spojitý matematický model meniča pozostávajúci z dvoch stavov,

(5.5)\[ \begin{align} \pmb{\dot{x}} = \frac{\mathrm{d} \, \pmb{x}}{\mathrm{d} t}=\pmb{A} \, \pmb{x}+ \pmb{B} \, \pmb{u}, \end{align} \]

(5.6)\[ \begin{align} \frac{\mathrm{d} }{\mathrm{d} t} \begin{pmatrix} i_L \end{pmatrix} = % \begin{pmatrix} -\frac{R}{L} \end{pmatrix} % \begin{pmatrix} i_L \end{pmatrix} + % \begin{pmatrix} \frac{1}{L} \end{pmatrix} % \begin{pmatrix} u_{s} \end{pmatrix}. \end{align} \]

(5.7)\[ \begin{align} \pmb{x} = \begin{pmatrix} i_L \end{pmatrix}, \, \pmb{u} = \begin{pmatrix} u_{s} \end{pmatrix}, \, \pmb{A} = \begin{pmatrix} -\frac{R}{L} \end{pmatrix}, \, \pmb{B} = \begin{pmatrix} \frac{1}{L} \end{pmatrix}. \end{align} \]

(5.8)\[ \begin{align} \frac{\mathrm{d} }{\mathrm{d} t} \begin{pmatrix} i_L \end{pmatrix} = % \begin{pmatrix} -\frac{R}{L} \end{pmatrix} % \begin{pmatrix} i_L \end{pmatrix}. \end{align} \]

(5.9)\[ \begin{align} \pmb{x} = \begin{pmatrix} i_L \end{pmatrix}, \, \pmb{A} = \begin{pmatrix} -\frac{R}{L} \end{pmatrix}. \end{align} \]

5.1.2. Matlab/Octave

Ukáž kód

% prudovy usmernovac
clc
clear all
close all

% parametre obvodu
U=100;
L=100e-3;
R=10;
f=50;

% krok simulacie
dt=1e-6;
% simulacny cas
Tsim=0.15;

w=2*pi*f;

% stavove matice
A=[-R/L];

B=[1/L];

% matice nepriamej eulerovej metody
F=inv(eye(size(A))-dt*A);
G=F*dt*B;

iL=0;% pociatocne podmienky
X=[iL];

n=1;
% nepriama eulerova metoda 
for t = 0:dt:Tsim
        us=U*sin(w*t);
        
        if us < 0
            us=0;
        end
        
        u = [us];

        X=F*X+G*u;
        iL(n)=X;
        us2(n) = us; 
        time(n)=t;
        n=n+1;
end

% priebehy
plot(time,iL*10,time,us2)
title('Priebehy obvodu');
legend('10*iL','uS');
ylabel('u [V], i [A]');
xlabel('t [s]');
grid on

Online simulácia

Spustiť simuláciu

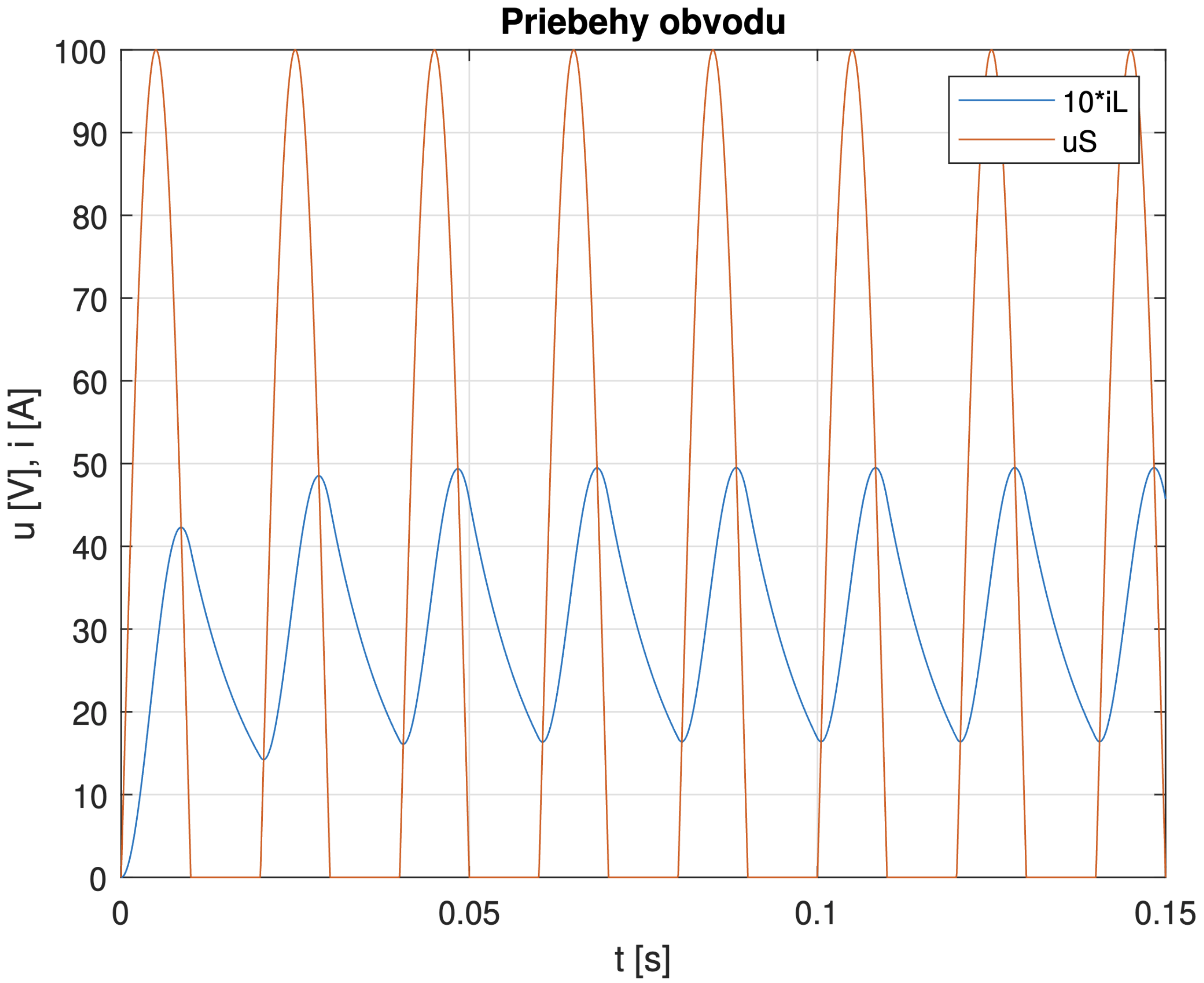
Obr. 5.4 Priebehy elektrických veličín prúdového usmerňovača.