3.1. Stavový opis dynamického systému

Každý fyzikálny systém (elektrický, mechanický, ekonomický, chemický, biologický, atď.) môžeme reprezentovať pomocou matematického modelu, ktorý má jeden alebo viac vstupov a výstupov [BV19]. Z pohľadu dynamiky môžeme rozdeliť systémy na systémy s dynamikou a bez dynamiky. Systémy bez dynamiky sú systémy, ktoré nemajú vnútornú pamäť (neobsahujú prvky akumulujúce energiu) a ich aktuálny výstup závisí len na jeho vstupe.

Príkladom môže byť jednoduchý elektrický obvod, kde je odpor \(R\) pripojený k zdroju napätia. Napätie \(u_R\) predstavuje vstup do systému a prúd \(i_R\) je jeho výstup,

(3.1)\[ i_R(t) = \frac{1}{R} \, u_R(t). \]

Systémy s dynamikou (dynamické systémy), sú systémy, ktoré majú vnútornú pamäť (majú prvky akumulujúce energiu) a ich aktuálny výstup nezávisí len od aktuálneho vstupu ale aj od prechádzajúcich stavov systému.

Príkladom može byť kondenzátor s kapacitou \(C\), kde vstupom do systému je prúd \(i_C\) a jeho výstupom je napätie \(u_C\) na kondenzátore,

(3.2)\[ u_C(t) = \frac{1}{C} \int_{t_0}^t i_C(\tau) \, \mathrm{d} \tau + u_C(t_0). \]

Ďalším príkladom je cievka s indukčnostou \(L\), kde vstupom do systému je napätie \(u_L\) a jeho výstupom je prúd \(i_L\),

(3.3)\[ i_L(t) = \frac{1}{L} \int_{t_0}^t u_L(\tau) \, \mathrm{d} \tau + i_L(t_0). \]

3.1.1. Obecný opis systému

Matematický model fyzikálneho dynamického systému opisujeme pomocou sústavy diferenciálnych a algebrických rovníc, ktoré nazývame stavové rovnice.

Pri nasledujúcom stavovom opise systému predpokladajme spojitý čas \(t \in \mathbb{R}\). Najskôr definujme stavový vektor \(\mathbf{x}(t)\), vektor vstupov \(\mathbf{u}(t)\) a vektor výstupov \(\mathbf{y}(t)\), ktoré sú funkciami času.

Stavový vektor \(\mathbf{x}(t) \in \mathbb{R}^n\), \(n \in \mathbb{N}\) je sĺpcový vektor, ktorý obsahuje \(n\) stavových premenných \(n\)-tého rádu systému. Pre elektrický sýstém to budú fyzikálne veličiny prvkov akumulujúcich energiu v systéme, t. j. napätia na kondenzátoroch a prúdy v cievkach elektrického obvodu,

(3.4)\[\begin{split} \mathbf{x}(t) = \begin{pmatrix} x_1(t)\\ x_2(t)\\ \vdots\\ x_n(t) \end{pmatrix}. \end{split}\]

Vektor vstupov \(\mathbf{u}(t) \in \mathbb{R}^m\), \(m \in \mathbb{N}\) je sĺpcový vektor, ktorý obsahuje vstupné veličiny budiace sýstém, t. j. veličiny dodávajúce energiu do systému,

(3.5)\[\begin{split} \mathbf{u}(t) = \begin{pmatrix} u_1(t)\\ u_2(t)\\ \vdots\\ u_m(t) \end{pmatrix}. \end{split}\]

Vektor výstupov \(\mathbf{y}(t)\in \mathbb{R}^p\), \(p \in \mathbb{N}\) je tvorený výstupnými veličinami systému.

(3.6)\[\begin{split} \mathbf{y}(t) = \begin{pmatrix} y_1(t)\\ y_2(t)\\ \vdots\\ y_p(t) \end{pmatrix}. \end{split}\]

U vektorov vstupov a výstupov u elektrického systému ide tiež o fyzikálne veličiny napätí a prúdov v elektrickom obvode. Ďalej popíšeme sústavu stavových rovníc systému.

Prvý typ stavových rovníc predstavuje differenciálne rovnice prvého rádu.

(3.7)\[\begin{split} \begin{split} \frac{\mathrm{d} x_1(t)}{\mathrm{d}t} &= f_1(x_1(t),x_2(t),\dots,x_n(t), u_1(t),u_2(t),\dots,u_m(t),t), \\ \frac{\mathrm{d} x_2(t)}{\mathrm{d}t} &= f_2(x_1(t),x_2(t),\dots,x_n(t), u_1(t),u_2(t),\dots,u_m(t),t), \\ & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \vdots \\ \frac{\mathrm{d} x_n(t)}{\mathrm{d}t} &= f_n(x_1(t),x_2(t),\dots,x_n(t), u_1(t),u_2(t),\dots,u_m(t),t). \end{split} \end{split}\]

Druhý typ stavových rovníc má algebrický tvar

(3.8)\[\begin{split} \begin{split} y_1(t) &= g_1(x_1(t),x_2(t),\dots,x_n(t), u_1(t),u_2(t),\dots,u_m(t),t), \\ y_2(t) &= g_2(x_1(t),x_2(t),\dots,x_n(t), u_1(t),u_2(t),\dots,u_m(t),t),\\ & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \vdots \\ y_p(t) &= g_r(x_1(t),x_2(t),\dots,x_n(t), u_1(t),u_2(t),\dots,u_m(t),t). \end{split} \end{split}\]

Obe stavové rovnice možeme zapísať aj vo vektorovom tvare

(3.9)\[\begin{split} \begin{split} \frac{\mathrm{d} \mathbf{x}(t)}{\mathrm{d}t} &= \mathbf{f}(\mathbf{x}(t),\mathbf{u}(t),t), \\ \mathbf{y} &= \mathbf{g}(\mathbf{x}(t),\mathbf{u}(t),t), \end{split} \end{split}\]

kde \(\mathbf{f}(\cdot)\) je stĺpcový vektor lineárnych alebo nelineárnych funkcií hodnôt stavov \(\mathbf{x}\), vstupov systému \(\mathbf{u}\) a času \(t\), ktoré sa rovnajú deriváciam stavových premenných,

(3.10)\[\begin{split} \mathbf{f}(\cdot) = \begin{pmatrix} f_1(\cdot)\\ f_2(\cdot)\\ \vdots\\ f_n(\cdot) \end{pmatrix} \end{split}\]

a stĺpcový vektor \(\mathbf{g}(\cdot)\) znova obsahuje lineárne alebo nelineárne funkie, ktoré určujú hodnotu výstupných veličín systému,

(3.11)\[\begin{split} \mathbf{g}(\cdot) = \begin{pmatrix} g_1(\cdot)\\ g_2(\cdot)\\ \vdots\\ g_n(\cdot) \end{pmatrix}. \end{split}\]

Ide o najobecnejši opis dynamického systému platný pre lineárne aj nelineárne dynamické systémy (lineárne aj nelineárne differenciálne rovnice) a pre tzv. časovo variantný systém t. j. systém, ktorého parametre a aj štruktúra sa môžu meniť v čase. Ak sa parametre systému nemenia, ide o tzv. časovo invariantný systém a môžeme jeho stavový opis zapísať v tvare

(3.12)\[\begin{split} \begin{split} \frac{\mathrm{d} \mathbf{x}(t)}{\mathrm{d}t} &= \mathbf{f}(\mathbf{x}(t),\mathbf{u}(t)), \\ \mathbf{y}(t) &= \mathbf{g}(\mathbf{x}(t),\mathbf{u}(t)). \end{split} \end{split}\]

3.1.2. Opis lineárneho systému

Ďalej sa budeme zaoberať lineárnymi dynamickými systémami, t. j. lineárnimi elektrickými a elektronickými výkonovými obvodmi. Pre lineárny dynamický systém s meniacimi sa parametrami existuje ďalši tvar zápisu stavových roníc.

Prvý typ sústavy stavových rovníc je znova tvorený differenciálnymi rovnicami prvého rádu,

(3.13)\[\begin{split} \begin{split} \frac{\mathrm{d} x_1(t)}{\mathrm{d}t} &= a_{11} \, x_1(t)+ \cdots+ a_{1n} \, x_n(t)+ b_{11} \, u_1(t)+ \cdots+ b_{1m} \, u_m(t),\\ \frac{\mathrm{d} x_2(t)}{\mathrm{d}t} &= a_{21} \, x_1(t)+ \cdots+ a_{2n} \, x_n(t)+ b_{21} \, u_1(t)+ \cdots+ b_{2m} \, u_m(t),\\ & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \vdots \\ \frac{\mathrm{d} x_n(t)}{\mathrm{d}t} &= a_{n1} \, x_1(t)+ \cdots+ a_{nn} \, x_n(t)+ b_{n1} \, u_1(t)+ \cdots+ b_{nm} \, u_m(t).\\ \end{split} \end{split}\]

Druhý typ stavových rovníc má algebrický tvar

(3.14)\[\begin{split} \begin{split} y_1 &= c_{11} \, x_1(t)+ \cdots+ c_{1n} \, x_n(t)+ d_{11} \, u_1(t)+ \cdots+ d_{1m} \, u_m(t),\\ y_2 &= c_{21} \, x_1(t)+ \cdots+ c_{2n} \, x_n(t)+ d_{21} \, u_1(t)+ \cdots+ d_{2m} \, u_m(t),\\ & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \vdots \\ y_p &= c_{p1} \, x_1(t)+ \cdots+ c_{pn} \, x_n(t)+ d_{p1} \, u_1(t)+ \cdots+ d_{pm} \, u_m(t).\\ \end{split} \end{split}\]

Tieto stavové rovnice môžeme zapísať vo vektorovo-maticovom tvare

(3.15)\[\begin{split} \begin{split} \frac{\mathrm{d} \mathbf{x}(t)}{\mathrm{d}t} &= \mathbf{A}(t) \, \mathbf{x}(t) + \mathbf{B}(t) \,\mathbf{u}(t), \\ \mathbf{y}(t) &= \mathbf{C}(t) \, \mathbf{x}(t) + \mathbf{D}(t)\, \mathbf{u}(t). \end{split} \end{split}\]

Ak ide o lineárny časovo invariatný systém, alebo v skratke LTI systém (z anglického znenia linear time invariant system), môžeme ho zapísať pomocou nasledujúcich stavových rovníc

(3.16)\[\begin{split} \begin{split} \frac{\mathrm{d} \mathbf{x}(t)}{\mathrm{d}t} &= \mathbf{A} \, \mathbf{x}(t) + \mathbf{B} \,\mathbf{u}(t), \\ \mathbf{y}(t) &= \mathbf{C} \, \mathbf{x}(t) + \mathbf{D} \, \mathbf{u}(t). \end{split} \end{split}\]

Prvá rovnica opisuje, ako sa stavové premenné menia v závislosti na čase a vstupných premenných. Druhá rovnica opisuje, ako sa výstupné premenné menia v závislosti na stavových a vstupných premenných.

Matica \(\mathbf{A}(t) \in \mathbb{R}^{n \times n}\) je štvorcová matica o rozmeroch \(n \times n\). Je nazývaná stavová matica, systémová matica, alebo matica vnútorných väzieb systému.

(3.17)\[\begin{split} \mathbf{A}(t) = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{pmatrix}. \end{split}\]

Matica \(\mathbf{B}(t) \in \mathbb{R}^{n \times m}\) je matica o rozmeroch \(n \times m\). Je nazývaná vstupná matica alebo matica väzieb systému na vstup,

(3.18)\[\begin{split} \mathbf{B}(t) = \begin{pmatrix} b_{11} & b_{12} & \cdots & b_{1m} \\ b_{21} & b_{22} & \cdots & b_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ b_{n1} & b_{n2} & \cdots & b_{nm} \end{pmatrix}. \end{split}\]

Matica \(\mathbf{C}(t) \in \mathbb{R}^{p \times n}\) je matica o rozmeroch \(p \times n\). Je nazývaná výstupná matica, alebo matica väzieb výstupu na stav,

(3.19)\[\begin{split} \mathbf{C}(t) = \begin{pmatrix} c_{11} & c_{12} & \cdots & c_{1n} \\ c_{21} & c_{22} & \cdots & c_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ c_{p1} & c_{p2} & \cdots & c_{pn} \end{pmatrix}. \end{split}\]

Matica \(\mathbf{D}(t) \in \mathbb{R}^{p \times m}\) je matica o rozmeroch \(p \times m\). Je nazývaná matica priamej väzby medzi vstupom a výstupom, alebo matica prevodu,

(3.20)\[\begin{split} \mathbf{D}(t) = \begin{pmatrix} d_{11} & d_{12} & \cdots & d_{1m} \\ d_{21} & d_{22} & \cdots & d_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ d_{p1} & d_{p2} & \cdots & d_{pm} \end{pmatrix}. \end{split}\]

Bloková schéma lineárneho systému je znázornená na Obr. 3.1.

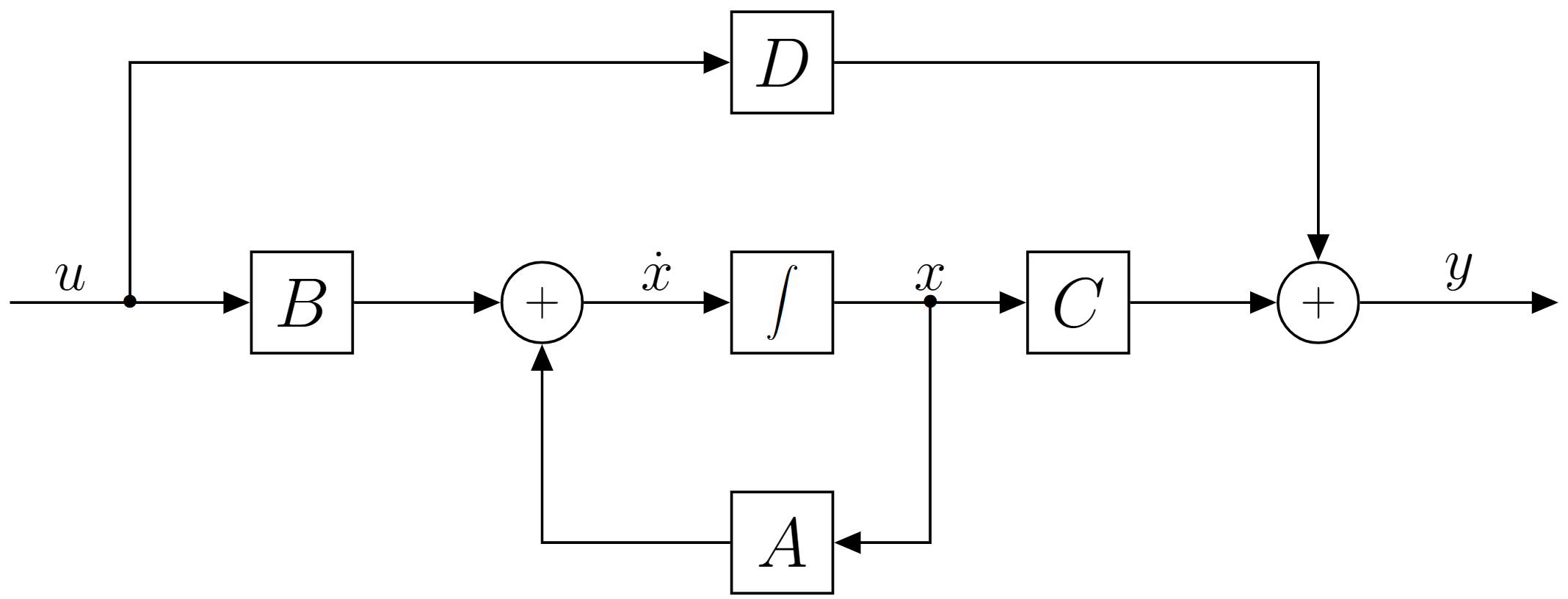
Obr. 3.1 Bloková schéma stavového popisu lineárneho systému.