Všeobecný elektrický obvod

Obsah

4.2. Všeobecný elektrický obvod#

Pri riešení tohto príkladu postupujeme rovnako ako v predchádzajúcom príklade.

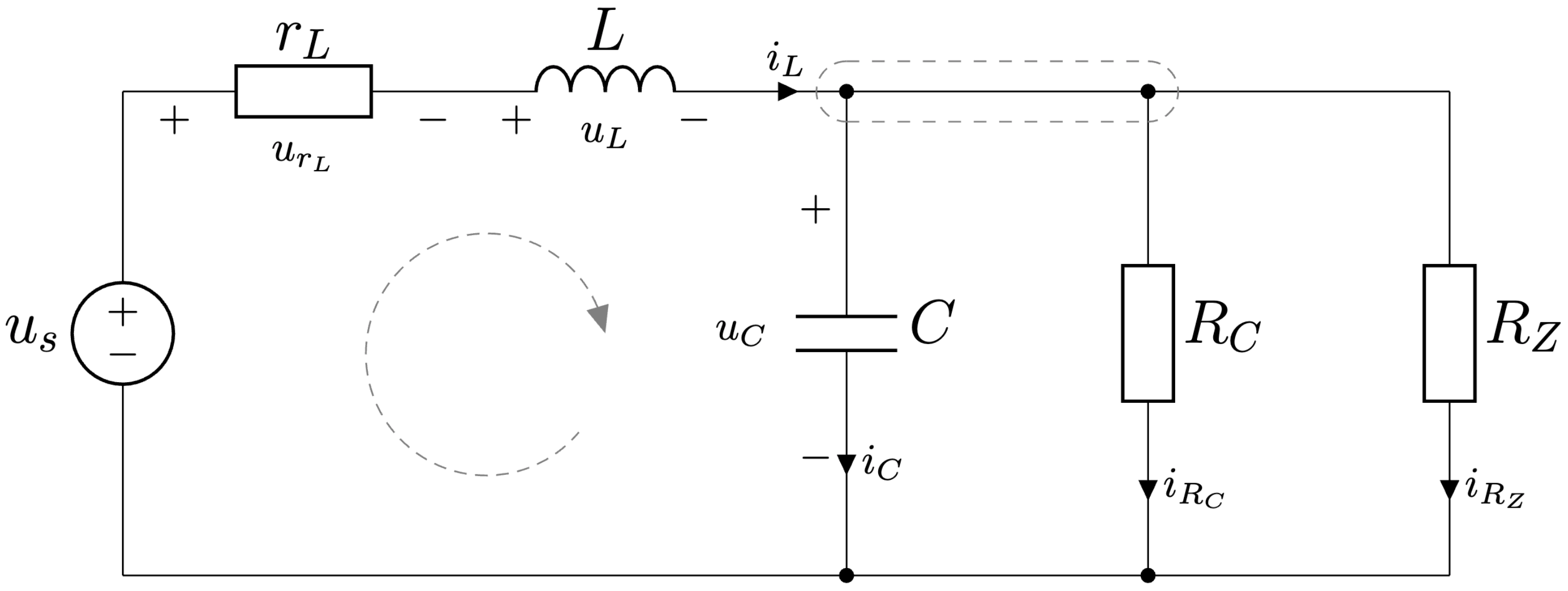
../../../_images/general_circuit_2.png — Obr. 4.2 Elektrický obvod.#

Najprv použijeme druhý Kirchhoffov zákon na získanie prvej diferenciálnej rovnice

(4.7)#\[\begin{split} \begin{align} \begin{split} -u_{s} + u_{r_L}+u_L + u_C &= 0, \\ -u_{s} + r_L \, i_L+L \frac{\mathrm{d} i_L}{\mathrm{d} t} + u_C &= 0, \\ L \frac{\mathrm{d} i_L}{\mathrm{d} t} &= -r_L \, i_L-u_C + u_{s}, \\ \frac{\mathrm{d} i_L}{\mathrm{d} t} &= -\frac{r_L}{L}\, i_L-\frac{1}{L} u_C + \frac{1}{L} u_{s}. \end{split} \end{align} \end{split}\]

Ďalej použijeme prvý Kirchhoffov zákon na získanie druhej diferenciálnej rovnice

(4.8)#\[\begin{split} \begin{align} \begin{split} -i_L +i_C +i_{R_C}+i_{R_Z} &= 0, \\ -i_L + C \frac{\mathrm{d} u_C}{\mathrm{d} t} + \frac{1}{R_C} u_C + \frac{1}{R_Z} u_C&= 0, \\ C \frac{\mathrm{d} u_C}{\mathrm{d} t} &= i_L - \frac{1}{R_C} u_C - \frac{1}{R_Z} u_C, \\ \frac{\mathrm{d} u_C}{\mathrm{d} t} &= \frac{1}{C} i_L - \frac{1}{R_C \, C} u_C - \frac{1}{R_Z \, C} u_C, \\ \frac{\mathrm{d} u_C}{\mathrm{d} t} &= \frac{1}{C} i_L - \left(\frac{1}{R_C} + \frac{1}{R_Z}\right) \frac{1}{C}u_C, \\ \frac{\mathrm{d} u_C}{\mathrm{d} t} &= \frac{1}{C} i_L - \frac{1}{R \, C} u_C. \end{split} \end{align} \end{split}\]

(4.9)#\[ \begin{align} \frac{1}{R} = \left(\frac{1}{R_C} + \frac{1}{R_Z}\right). \end{align} \]

4.2.1. Stavový opis#

Získané diferenciálne rovnice prevedieme do maticového stavu

(4.10)#\[\begin{split} \begin{align} \begin{split} \frac{\mathrm{d} i_L}{\mathrm{d} t} &= -\frac{r_L}{L}\, i_L-\frac{1}{L} u_C + \frac{1}{L} u_{s}, \\ \frac{\mathrm{d} u_C}{\mathrm{d} t} &= \frac{1}{C} i_L - \frac{1}{R \, C} u_C. \end{split} \end{align} \end{split}\]

(4.11)#\[ \begin{align} \pmb{\dot{x}} = \frac{\mathrm{d} \, \pmb{x}}{\mathrm{d} t}=\pmb{A} \, \pmb{x}+ \pmb{B} \, \pmb{u}, \end{align} \]

(4.12)#\[\begin{split} \begin{align} \frac{\mathrm{d} }{\mathrm{d} t} \begin{pmatrix} i_L \\ u_C \end{pmatrix} = % \begin{pmatrix} -\frac{r_L}{L} & - \frac{1}{L} \\ \frac{1}{C} & -\frac{1}{R \, C} \end{pmatrix} % \begin{pmatrix} i_{L} \\ u_{C} \end{pmatrix} + % \begin{pmatrix} \frac{1}{L} \\ 0 \end{pmatrix} % u_{s} . \end{align} \end{split}\]

(4.13)#\[\begin{split} \begin{align} \pmb{x} = \begin{pmatrix} i_L \\ u_C \end{pmatrix}, \, \pmb{u} = u_{s}, \, \pmb{A} = \begin{pmatrix} -\frac{r_L}{L} & - \frac{1}{L} \\ \frac{1}{C} & -\frac{1}{R \, C} \end{pmatrix}, \, \pmb{B} = \begin{pmatrix} \frac{1}{L} \\ 0 \end{pmatrix}. \end{align} \end{split}\]

4.2.2. Matlab/Octave#

Ukáž kód

% elektricky obvod
clc
clear all
close all

% parametre obvodu
rL=1e-3;
rC=5e6;
us=10;
L=10e-6;
C=10e-6;
Rz=100;

% krok simulacie
dt=1e-6;
% simulacny cas
Tsim=0.001;

R=(Rz*rC)/(rC+Rz);

% stavove matice
A=[-rL/L  -1/L;
  1/C    -1/(C*R)];

B=[1/L  0;
  0   0];

u=[us;0];

% matice nepriamej eulerovej metody
F=inv(eye(size(A))-dt*A);

G=F*dt*B;

% pociatocne podmienky
iL=0;
uC=0;
x=[iL;uC];

n=1;
% nepriama eulerova metoda   
for t = 0:dt:Tsim
  x=F*x+G*u;
  iL(n)=x(1);
  uC(n)=x(2);
  time(n)=t;
  n=n+1;
end

iC=(iL-(uC/R));
iR=uC/Rz;

% priebehy
figure 
subplot(4,1,1)
plot(time,uC)
ylabel('uC [V]');
xlabel('t [s]');
grid on

subplot(4,1,2)
plot(time,iL)
ylabel('iL [A]');
xlabel('t [s]');
grid on

subplot(4,1,3)
plot(time,iC)
ylabel('iC [A]');
xlabel('t [s]');
grid on

subplot(4,1,4)
plot(time,iR)
ylabel('iR [A]');
xlabel('t [s]');
grid on

Online simulácia

Spustiť simuláciu

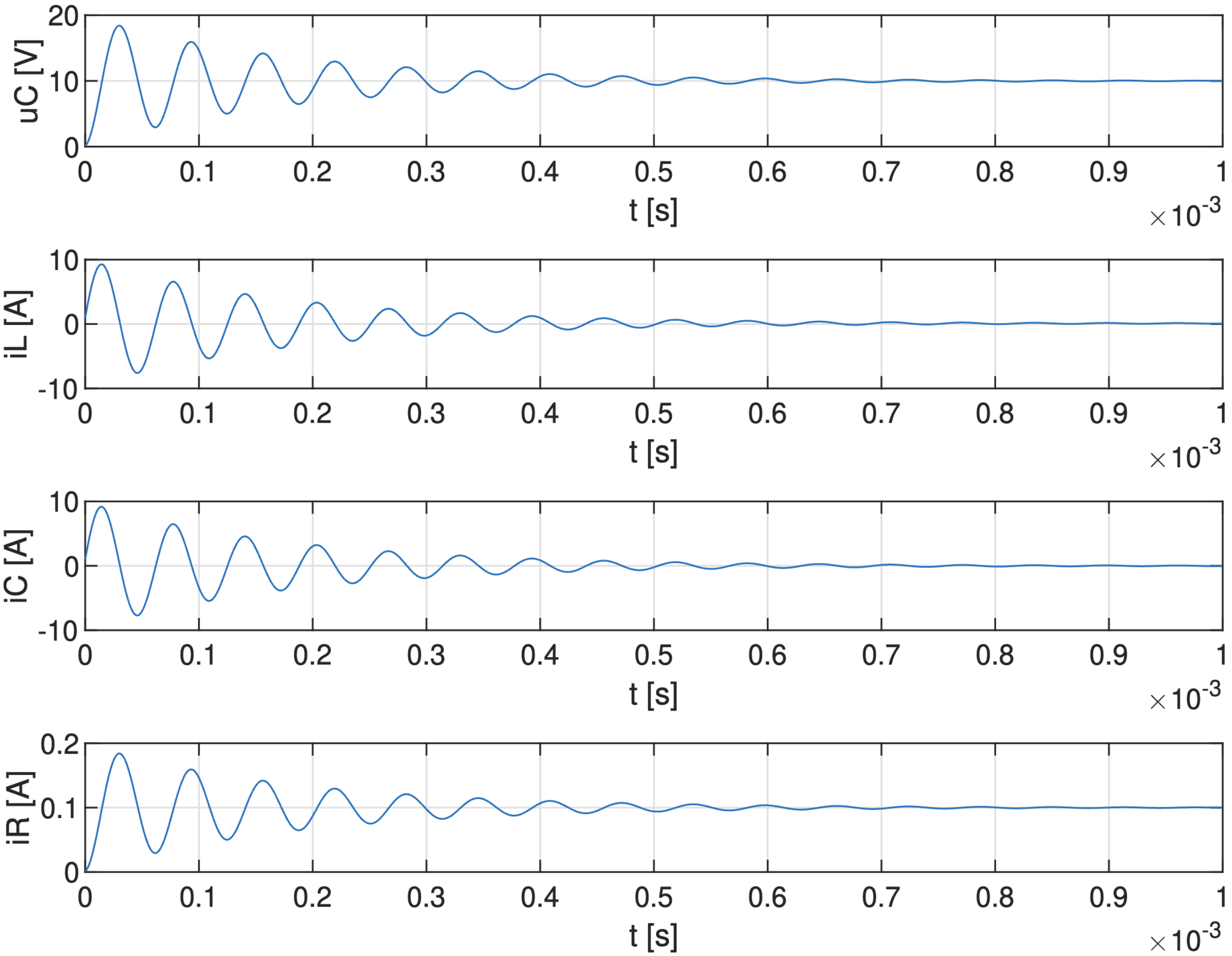
../../../_images/plot_vseob.png — Obr. 4.3 Priebehy elektrických veličín.#