5.2. Napäťové usmerňovače - usmerňovače s kapacitným filtrom

Princíp činnosti usmerňovačov s kapacitným filtrom je všeobecne založený na podmienke, že ak je vstupné sieťové napätie \(u_s(t)\) väčšie ako napätie na filtračnom kondenzátore \(C\), nastáva aktívny interval. Počas tohto intervalu sú diódy vodivé a kondenzátor \(C\) sa nabíja a jeho napätie narastá, teda nastáva tok energie zo siete do záťaže a do kondenzátora na jeho nabíjanie. Prúd obsahuje veľa neharmonických zložiek, pričom najvýznamnejšia je 3, 5 a 7.

V okamihu, keď je vstupné sieťové napätie \(u_s(t)\) rovnaké, alebo menšie ako napätie na filtračnom kondenzátore \(C\) nastáva neaktívny interval, diódy sa zatvoria a zdrojom energie pre pripojenú záťaž je len kondenzátor \(C\) a jedine on pokrýva potreby záťaže - nastáva pokles napätia na kondenzátore \(C\). Veľkosť kapacity filtračného kondenzátora ovplyvňuje zvlnenie výstupného napätia, ale aj tvar vstupného prúdu. Pre správnu činnosť meniča musíme korektne opísať všetky stavy jeho činnosti.

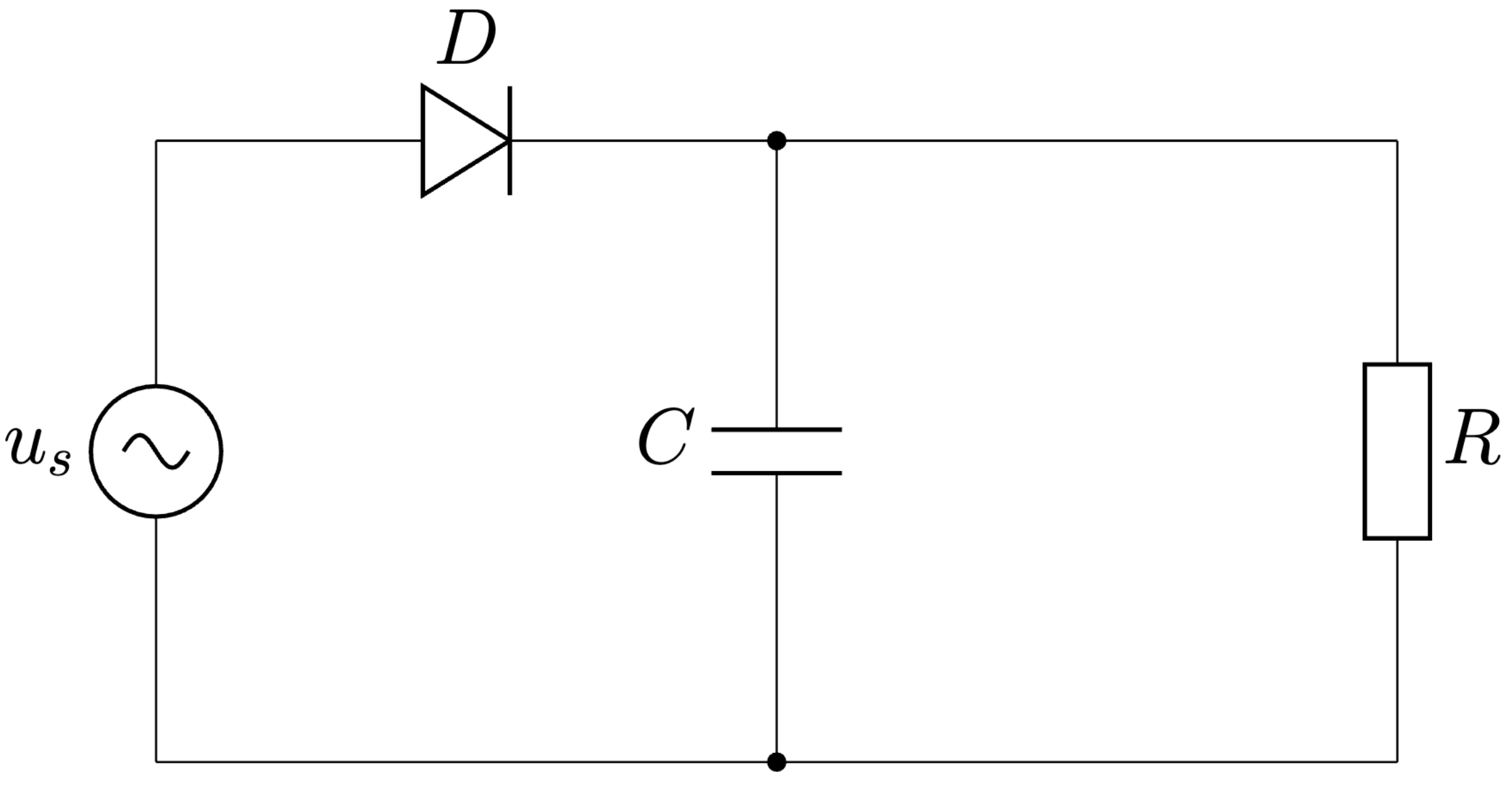
Obr. 5.5 Jednocestný usmerňovač s kapacitným filtrom.

5.2.1. Jednocestný usmerňovač s kapacitným filtrom

Ako už bolo spomenuté, princíp činnosti jednocestného usmerňovača s kapacitným filtrom, Obr. 5.5, je založený na podmienke, že ak je vstupné sieťové napätie \(u_s(t)\) väčšie ako napätie na filtračnom kondenzátore \(C\), dióda \(D\) sa otvorí, kondenzátor \(C\) sa nabíja, Obr. 5.6.

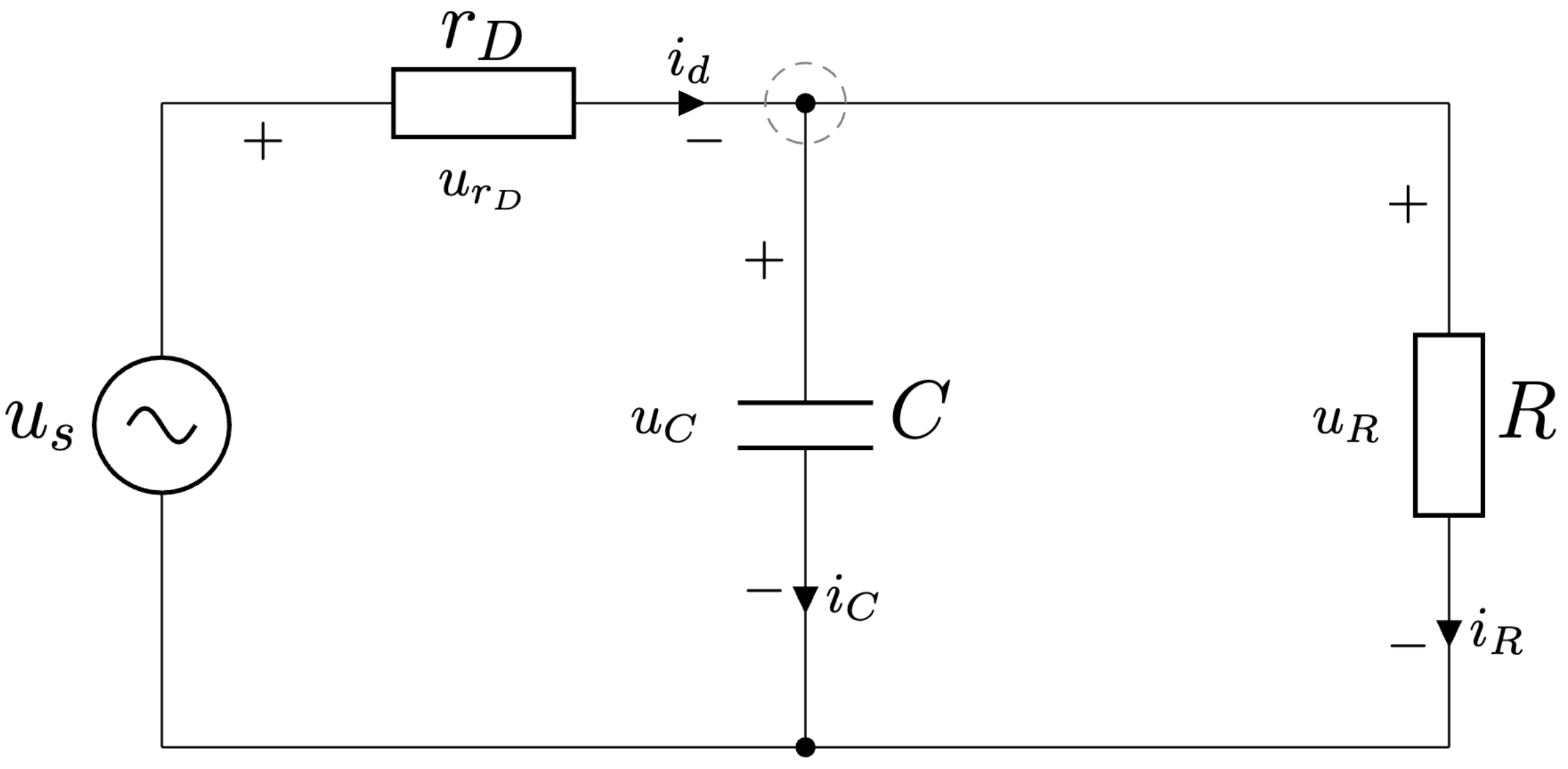
Obr. 5.6 Jednocestný usmerňovač s kapacitným filtrom - aktívny interval.

V okamihu, keď je vstupné sieťové napätie \(u_s(t)\) menšie ako napätie na filtračnom kondenzátore \(C\), dióda \(D\) sa zatvorí a len kondenzátor \(C\) pokrýva odber záťaže, Obr. 5.7. Nevýhodou tohoto zapojenia je, že veľkosť zvlnenia výstupného napätia je dosť vysoká, vzhľadom na to, že do výstupného kondenzátora je energia dodávaná iba počas kladnej periódy sieťového napätia.

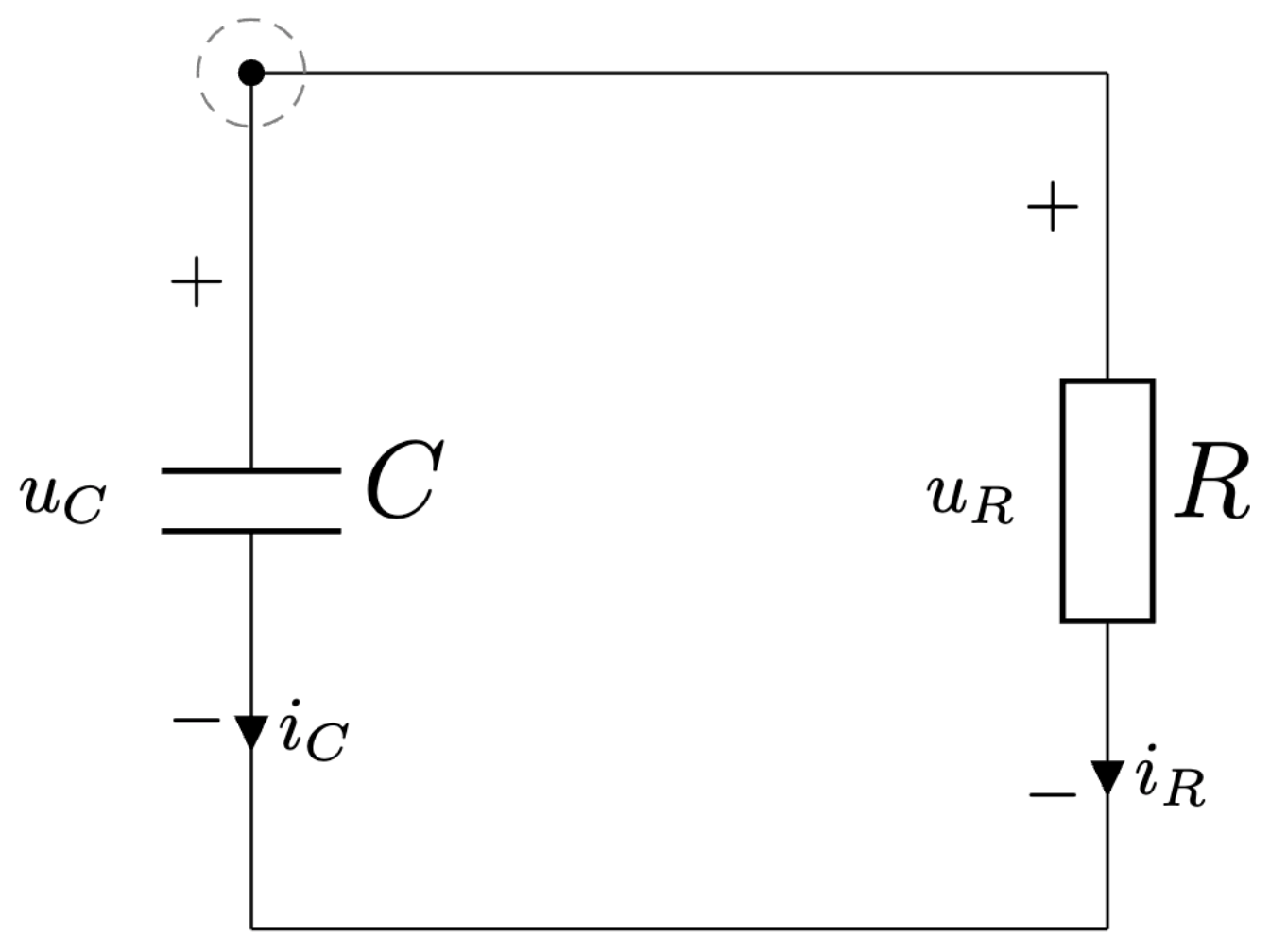
Obr. 5.7 Jednocestný usmerňovač s kapacitným filtrom - neaktívny interval.

Pre získanie diferenciálnej rovnice aktívneho intervalu použijeme prvý Kirchhoffov zákon.

(5.10)\[\begin{split} \begin{align} \begin{split} i -i_C - i_R &= 0, \\ \frac{u_{r_D}}{r_D} - C\, \frac{\mathrm{d} u_C}{\mathrm{d} t} - \frac{u_C}{R} &= 0, \\ \frac{u_S-u_C}{r_D} - C\, \frac{\mathrm{d} u_C}{\mathrm{d} t} - \frac{u_C}{R} &= 0, \\ - C\, \frac{\mathrm{d} u_C}{\mathrm{d} t} &= - \frac{u_S-u_C}{r_D} + \frac{u_C}{R}, \\ \frac{\mathrm{d} u_C}{\mathrm{d} t} &= \frac{1}{C} \left(\frac{u_S-u_C}{r_D} - \frac{u_C}{R} \right), \\ \frac{\mathrm{d} u_C}{\mathrm{d} t} &= \frac{1}{C} \left(\frac{u_S}{r_D} -\frac{u_C}{r_D} - \frac{u_C}{R} \right), \\ \frac{\mathrm{d} u_C}{\mathrm{d} t} &= \frac{1}{C} \left(- \frac{u_C}{R_x} + \frac{u_S}{r_D} \right), \\ \frac{\mathrm{d} u_C}{\mathrm{d} t} &= - \frac{1}{R_x\,C}\, u_C + \frac{1}{r_D\,C}\,u_S, \end{split} \end{align} \end{split}\]

kde

(5.11)\[ \begin{align} \frac{1}{R_x} = \frac{1}{R} + \frac{1}{r_D} = \frac{R+r_D}{R \, r_D}. \end{align} \]

Použijeme prvý Kirchhoffov zákon na získanie diferenciálnej rovnice druhého stavu.

(5.12)\[\begin{split} \begin{align} \begin{split} -i_C - i_R &= 0, \\ - C\, \frac{\mathrm{d} u_C}{\mathrm{d} t} - \frac{u_C}{R} &= 0, \\ - C\, \frac{\mathrm{d} u_C}{\mathrm{d} t} &= \frac{u_C}{R} , \\ \frac{\mathrm{d} u_C}{\mathrm{d} t} &= -\frac{1}{R \, C} \, u_C. \end{split} \end{align} \end{split}\]

5.2.2. Stavový opis

Získali sme diferenciálnu rovnicu pre prvý stav

(5.13)\[ \begin{align} \frac{\mathrm{d} u_C}{\mathrm{d} t} &= - \frac{1}{R_x\,C}\, u_C + \frac{1}{r_D\,C}\,u_S \end{align} \]

a pre druhý stav

(5.14)\[ \begin{align} \frac{\mathrm{d} u_C}{\mathrm{d} t} &= -\frac{1}{R \, C} \, u_C. \end{align} \]

(5.15)\[ \begin{align} \pmb{\dot{x}} = \frac{\mathrm{d} \, \pmb{x}}{\mathrm{d} t}=\pmb{A} \, \pmb{x}+ \pmb{B} \, \pmb{u}, \end{align} \]

(5.16)\[ \begin{align} \frac{\mathrm{d} }{\mathrm{d} t} \begin{pmatrix} u_C \end{pmatrix} = % \begin{pmatrix} - \frac{1}{R_x\,C} \end{pmatrix} % \begin{pmatrix} u_{C} \end{pmatrix} + % \begin{pmatrix} \frac{1}{r_D\,C} \end{pmatrix} % \begin{pmatrix} u_{s} \end{pmatrix}. \end{align} \]

(5.17)\[ \begin{align} \pmb{x} = \begin{pmatrix} u_C \end{pmatrix}, \, \pmb{u} = \begin{pmatrix} u_{s} \end{pmatrix}, \, \pmb{A_1} = \begin{pmatrix} - \frac{1}{R_x\,C} \end{pmatrix}, \, \pmb{B_1} = \begin{pmatrix} \frac{1}{r_D\,C} \end{pmatrix}. \end{align} \]

(5.18)\[ \begin{align} \frac{\mathrm{d} }{\mathrm{d} t} \begin{pmatrix} u_C \end{pmatrix} = % \begin{pmatrix} - \frac{1}{R\,C} \end{pmatrix} % \begin{pmatrix} u_{C} \end{pmatrix}. \end{align} \]

(5.19)\[ \begin{align} \pmb{x} = \begin{pmatrix} u_C \end{pmatrix}, \, % \pmb{u} = \begin{pmatrix} % u_{s} % \end{pmatrix}, \, \pmb{A_2} = \begin{pmatrix} - \frac{1}{R\,C} \end{pmatrix}%, \, \pmb{B_2} = \begin{pmatrix} 0 \end{pmatrix}. \end{align} \]

5.2.3. Matlab/Octave

Ukáž kód

% jednocestny usmernovac
clear all
clc
close all

% parametre obvodu
U=100;
C = 100e-6;
R=100;
f=50;
rd = 1e-3;

% krok simulacie
dt=1e-6;
% simulacny cas
Tsim=0.1;

w=2*pi*f;
Rx = (R*rd)/(R+rd);

% stavove matice
A1=[-1/(Rx*C)];
A2=[-1/(R*C)];
B1=[1/(rd*C)];
B2=[0];

% matice nepriamej eulerovej metody
F1=inv(eye(size(A1))-dt*A1);
G1=F1*dt*B1;

F2=inv(eye(size(A2))-dt*A2);
G2=F2*dt*B2;

% pociatocne podmienky
uc=0;
X=[uc];

n=1;
% nepriama eulerova metoda 
for t = 0:dt:Tsim
    
    u=U*sin(w*t);
    
    if u > X
        X=F1*X+G1*u;
        i(n) = (u-X)/rd;
    else
        X=F2*X+G2*u;
        i(n) = 0;
    end
    
    uc(n)=X;
    irz(n) = uc(n)/R;
    
    ic(n) = i(n) - irz(n);
    time(n)=t;
    us(n) = u;

    n=n+1;
end

% priebehy
plot(time,uc,time,us,time,irz*20)
title('Priebehy obvodu');
legend('uC','uS','20*irz');
ylabel('u [V], i [A]');
xlabel('t [s]');
grid on

Online simulácia

Spustiť simuláciu

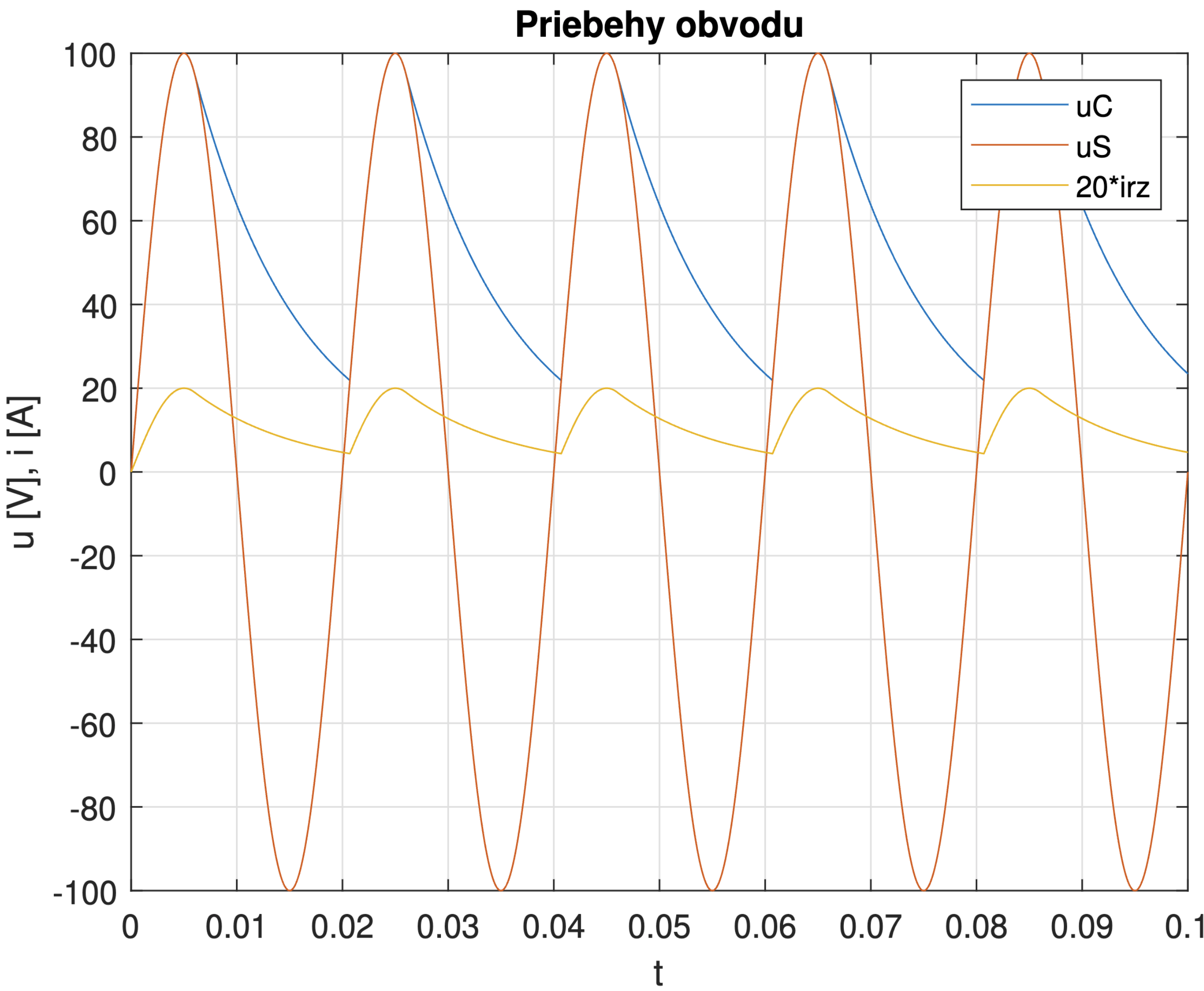
Obr. 5.8 Priebehy elektrických veličín jednocestného usmerňovača.

5.2.4. Mostový usmerňovač s kapacitným filtrom

Princíp činnosti napäťových usmerňovačov už bol spomenutý vyššie. Výhoda mostového zapojenia usmerňovača v porovnaní s jednocestným usmerňovačom je v tom, že zvlnenie výstupného napätia je nižšie, nakoľko v mostovom usmerňovači je energia do výstupného kondenzátora C dodávaná v oboch polperiódach vstupného napätia.

5.2.5. Matlab/Octave

Ukáž kód

% mostovy usmernovac
clc
clear all
close all

% parametre obvodu
U=230*sqrt(2);
C = 100e-6;
Rz=200;
f=50;
rd = 1e-3;

% krok simulacie
dt=1e-6;
% simulacny cas
Tsim=0.1;

w=2*pi*f;

R = (Rz*rd)/(Rz+rd);

% stavove matice
A1=[-1/(R*C)];
A2=[-1/(Rz*C)];
B1=[1/(rd*C)];
B2=[0];

% matice nepriamej eulerovej metody
F1=inv(eye(size(A1))-dt*A1);
G1=F1*dt*B1;

F2=inv(eye(size(A2))-dt*A2);
G2=F2*dt*B2;

% pociatocne podmienky
uc=0;
X=[uc];

n=1;
% nepriama eulerova metoda 
for t = 0:dt:Tsim
    u=abs(U*sin(w*t));
    
    if u > X
        X=F1*X+G1*u;
        i(n) = (u-X)/rd;
    else
        X=F2*X+G2*u;
        i(n) = 0;
    end

    i(n) = (u-X)/rd;
    uc(n)=X;
    irz(n) = uc(n)/Rz;
    ic(n) = i(n) - irz(n);
    time(n)=t;
    us(n) = u;
    n=n+1;
end

% priebehy
plot(time,uc,time,us,time,irz*100)
grid on
title('Priebehy obvodu');
legend('uC','uS','100*irz');
ylabel('u [V], i [A]');
xlabel('t [s]');
grid on

Online simulácia

Spustiť simuláciu

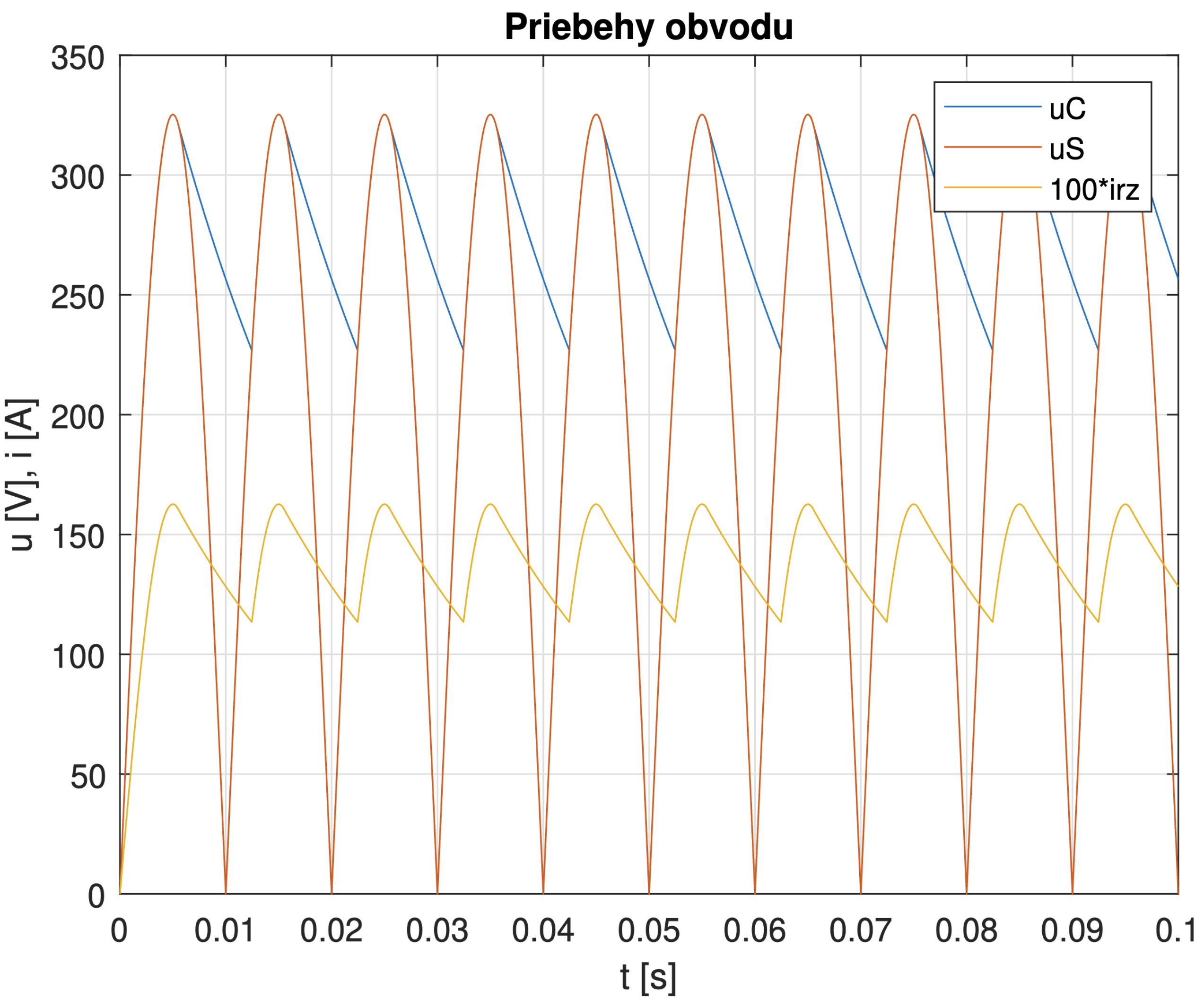
Obr. 5.9 Priebehy elektrických veličín dvojcestného usmerňovača.