Znižovací DC/DC menič (Buck)

Obsah

6.1. Znižovací DC/DC menič (Buck)#

Znižovací menič (Buck), Obr. 6.1, patrí do kategórie spínaných meničov. Ako už vyplýva z jeho názvu, je schopný vytvoriť na jeho výstupe nižšie napätie ako je na vstupe. Výhodou tohto typu spínaného zdroja v porovnaní s lineárnymi zdrojmi je oveľa vyššia účinnosť, a tým pádom oveľa menšie straty v podobe tepla, čo nám konštrukčne umožňuje vytvoriť spínané zdroje menších rozmerov a vyšších výkonov ako u lineárnych zdrojov.

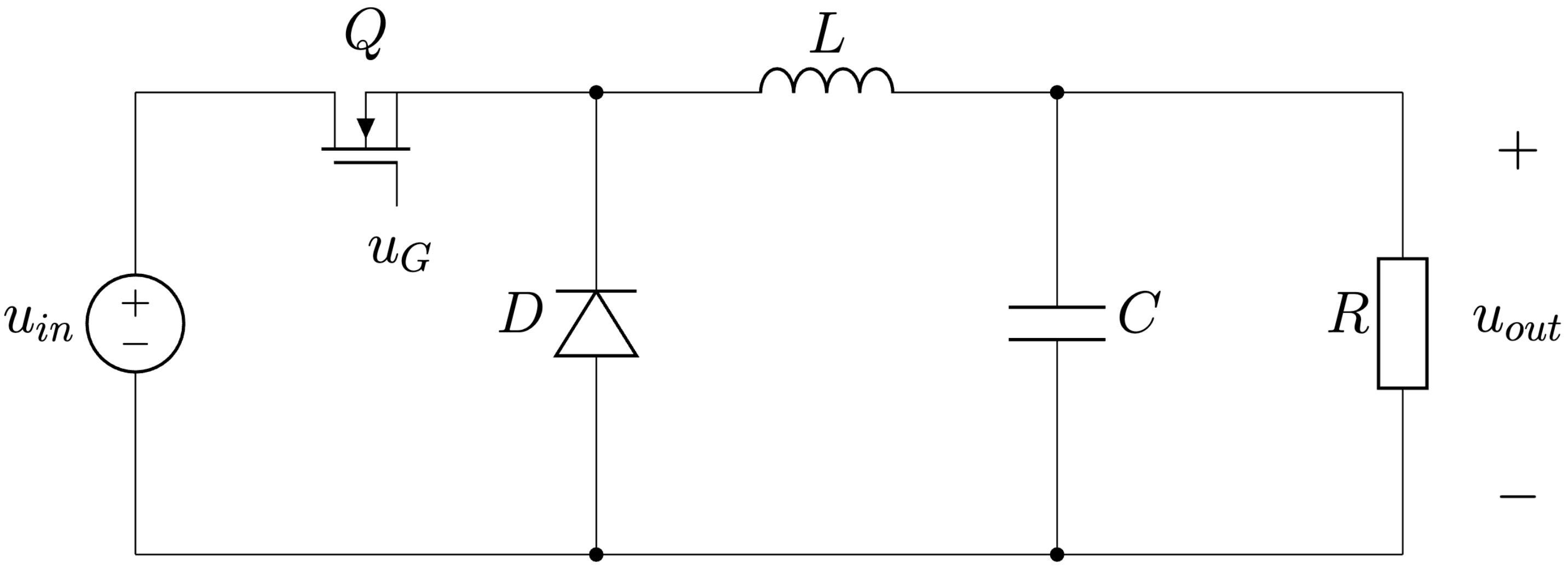
../../../_images/buck_ideal.png — Obr. 6.1 Znižovací menič (Buck).#

Tranzistor Q a dióda D slúžia ako spínače. Tranzistor Q je spínaný napätím \(u_G\) privedeným na Gate s impulznou šírkovou moduláciou (PWM) o frekvencii \(f\). Vždy je súčasne otvorený len jeden spínač, tranzistor alebo dióda. Ak je zopnutý tranzistor, dióda je polarizovaná v záverom smere. Ak je tranzistor rozopnutý, dióda je polarizovaná v priepustnom smere, uvažujeme ideálne spínacie prvky. Pre korektnú činnosť meniča je potrebné analyzovať všetky intervaly činnosti meniča.

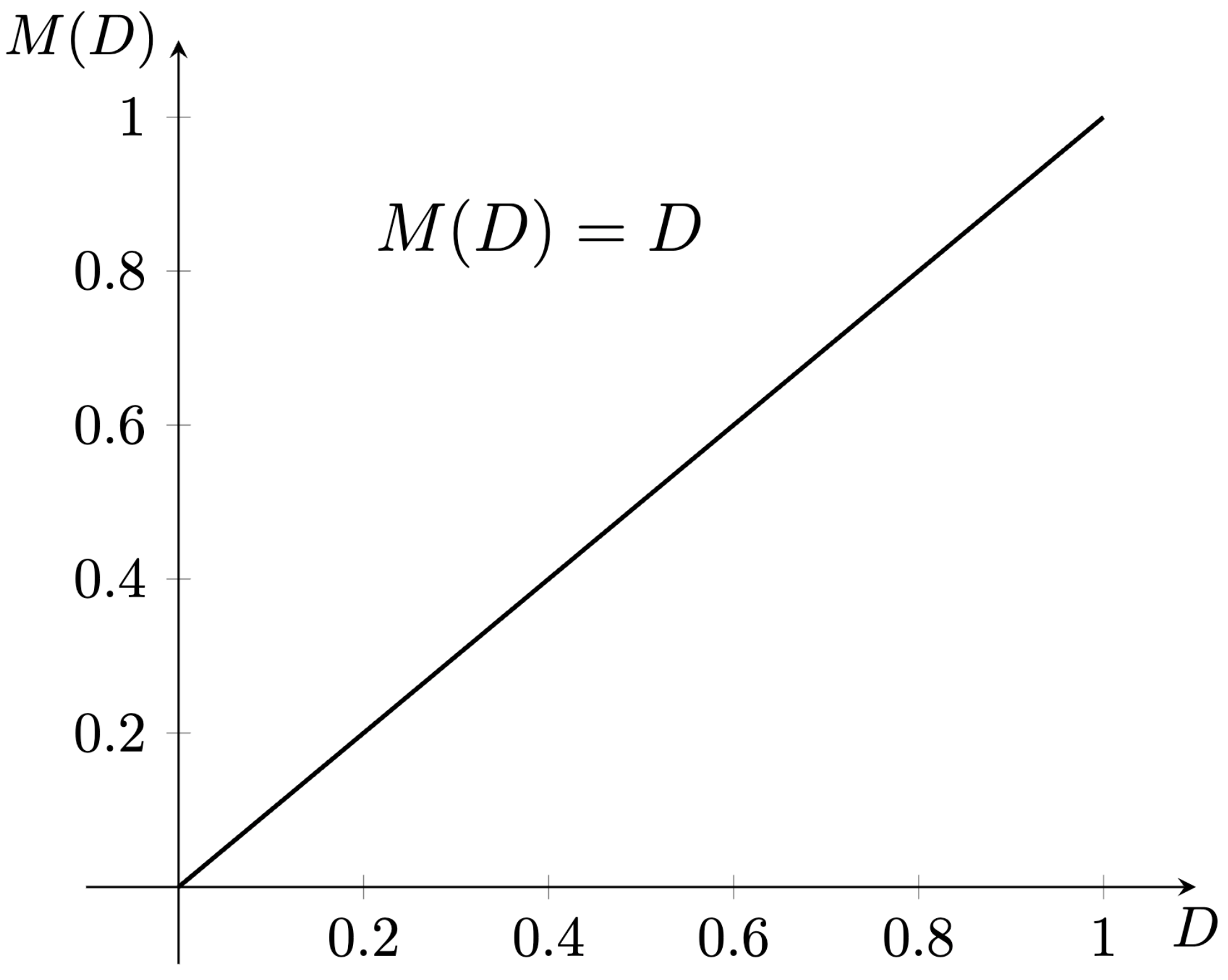
../../../_images/buck_conversion.png — Obr. 6.2 Prevodová charakteristika medzi vstupným a výstupný napätím ideálneho znižujúceho meniča.#

Hodnota výstupného napätia je daná nasledujúcim vzťahom

(6.1)#\[ \begin{align} %\label{eqn:uout} u_{out} = D \, u_{in}, \end{align} \]

kde \(u_{in}\) je vstupné napätie, \(u_{out}\) je výstupné napätie a \(D\) je pomerná širka zopnutia (strieda) tranzistora Q. Prevodová charakteristika je zobrazená na obrázku Obr. 6.2.

Šírkovú impulznú moduláciu potrebnú na ovládanie spínaného meniča môžeme vytvoriť porovnávaním vysokofrekvenčného trojuholníkového (pílového) priebehu s referenčnou hodnotou, ktorá predstavuje hodnotu pomernej šírky zopnutia \(D\) (hodnota 0 až 1), Obr. 6.3.

Hodnota pomernej šírky zopnutia je daná ako

(6.2)#\[ \begin{align} \label{eqn:duty} D = \frac{t_{on}}{T}, \end{align} \]

kde \(t_{on}\) čas trvania zopnutia tranzistora \(Q\) a \(T\) je perióda spínania.

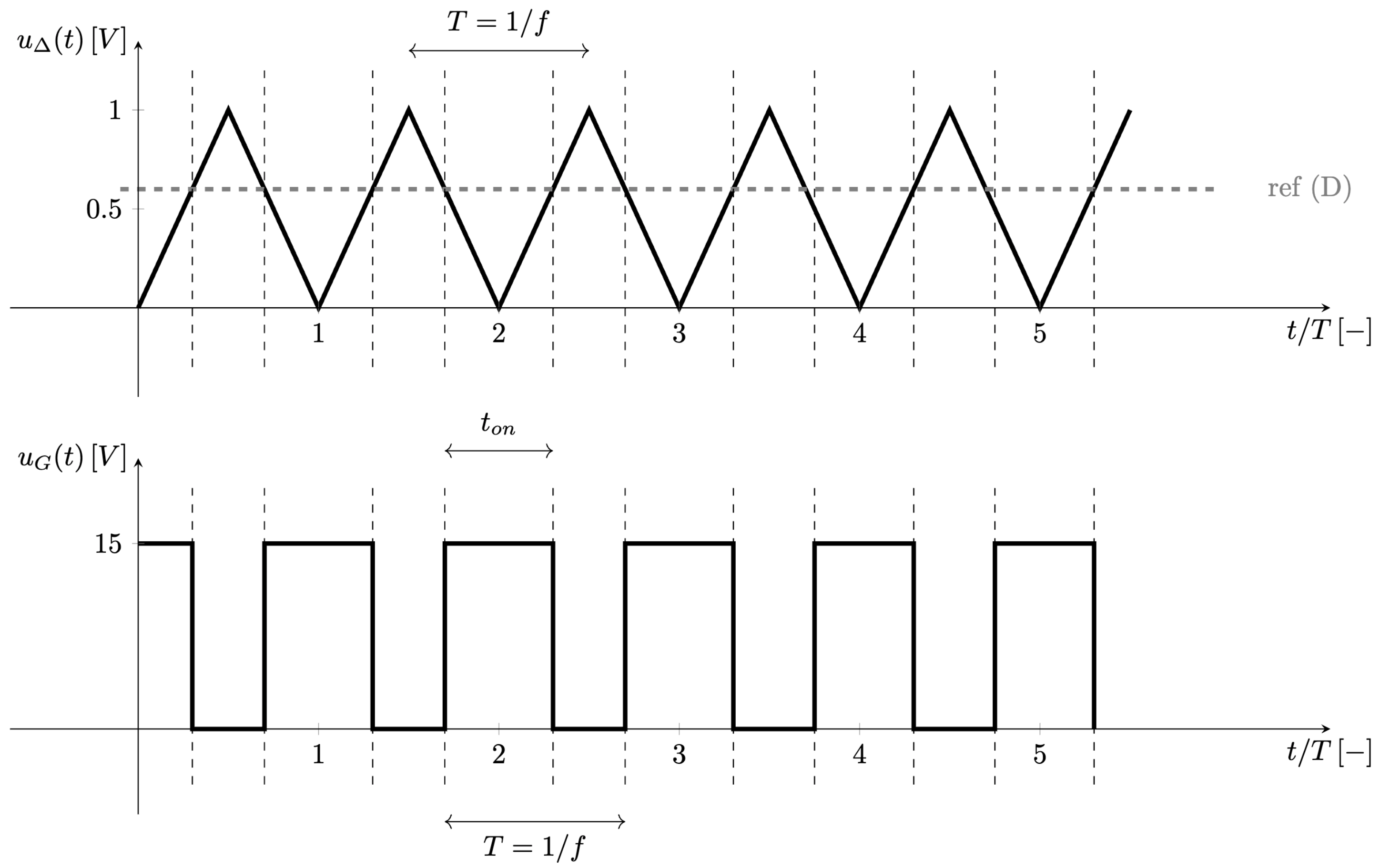
../../../_images/triangle.png — Obr. 6.3 Generovanie šírkovo impulznej modulácie.#

6.1.1. Analýza princípu činnosti znižovacieho meniča#

Princíp činnosti znižovacieho DC/DC meniča Buck je zjednodušene rozdelený do dvoch intervalov činnosti.

6.1.1.1. Prvý interval činnosti - aktívny interval#

V tomto aktívnom intervale činnosti je tranzistor zopnutý a dióda je polarizovaná v závernom smere. Energia zo vstupného zdroja sa akumuluje do indukčnosti \(L\) a kondenzátora \(C\) a zároveň je dodávaná do záťaže \(R\). Výsledná topológia je zobrazená na Obr. 6.4.

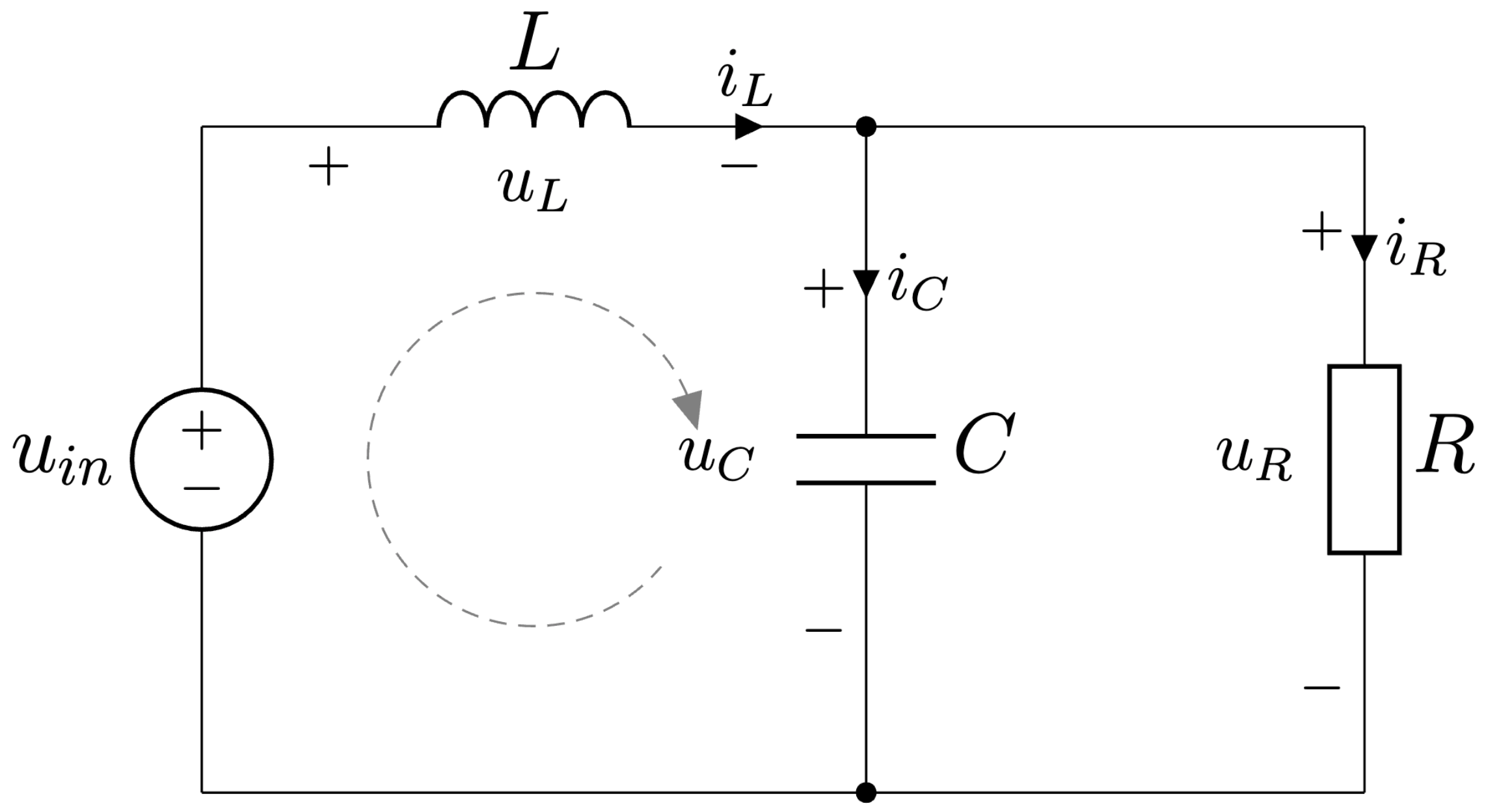
../../../_images/buck_state_1.png — Obr. 6.4 Znižovací menič Buck - aktívny interval.#

Najprv použijeme druhý Kirchhoffov zákon na získanie prvej diferenciálnej rovnice

(6.3)#\[\begin{split} \begin{align} \begin{split} -u_{in} + u_L + u_C &= 0, \\ -u_{in} + L \frac{di_L}{dt} + u_C &= 0, \\ L \frac{di_L}{dt} &= -u_C + u_{in}, \\ \frac{di_L}{dt} &= -\frac{1}{L} u_C + \frac{1}{L} u_{in}. \end{split} \end{align} \end{split}\]

Ďalej použijeme prvý Kirchhoffov zákon na získanie druhej diferenciálnej rovnice

(6.4)#\[\begin{split} \begin{align} \begin{split} i_L -i_C -i_R &= 0, \\ i_L - C \frac{du_C}{dt} - \frac{1}{R} u_C &= 0, \\ - C \frac{du_C}{dt} &= -i_L + \frac{1}{R} u_C, \\ \frac{du_C}{dt} &= \frac{1}{C} i_L - \frac{1}{R \, C} u_C. \end{split} \end{align} \end{split}\]

6.1.1.2. Druhý interval činnosti#

V druhom intervale činnosti je tranzistor vypnutý (obvod je odpojený od zdroja napätia) a dióda je vodivá - je polarizovaná v priepustnom smere. Energia z cievky \(L\) a kondenzátora \(C\) je dodávaná do záťaže \(R\) cez diódu \(D\). Výsledná topológia je zobrazená na Obr. 6.5.

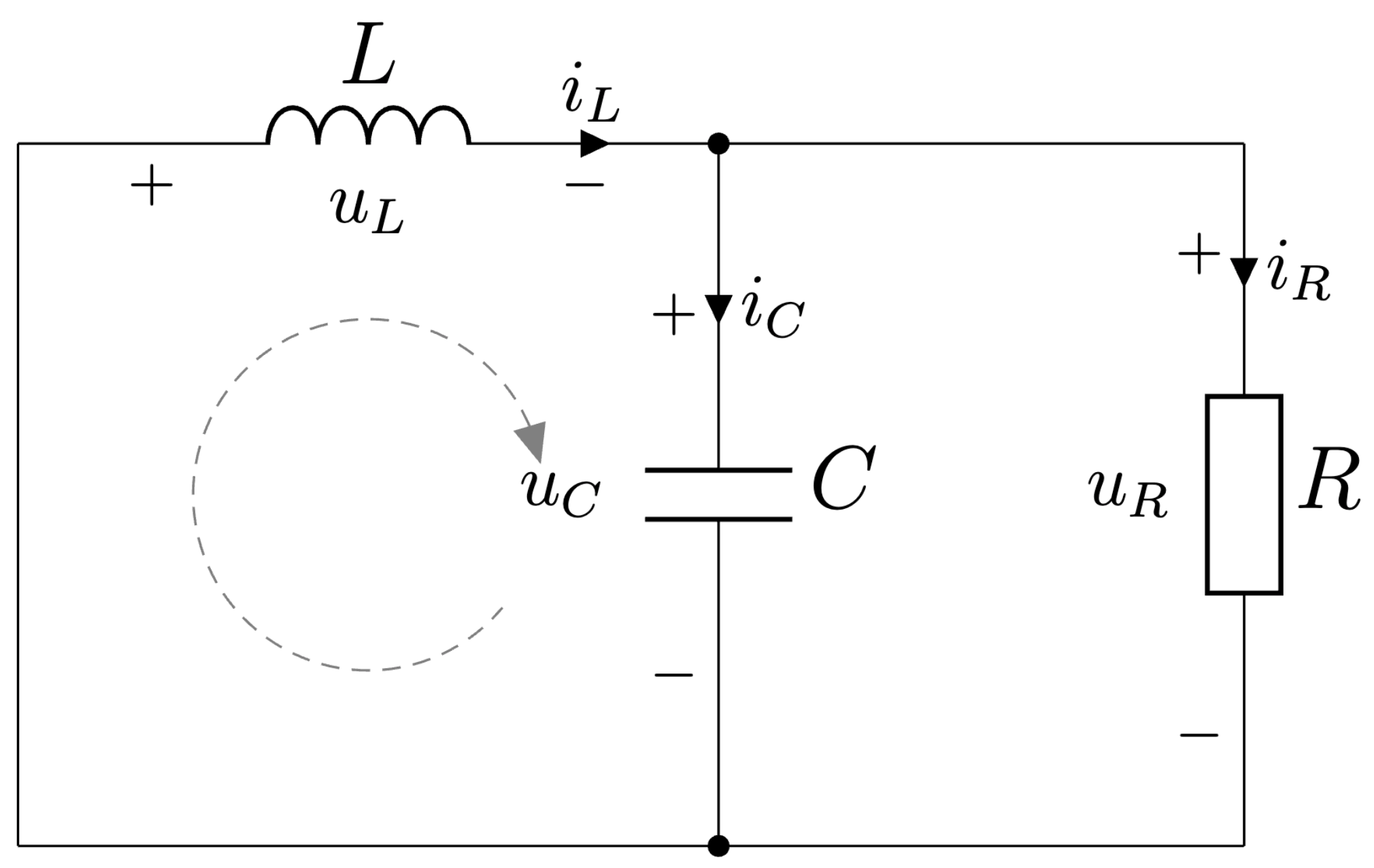
../../../_images/buck_state_2.png — Obr. 6.5 Znižovací menič Buck - neaktívny interval.#

Rovnice získame rovnakým spôsobom ako v predchádzajúcom intervale činnosti.
Prvá rovnica bude podobná, nebude však obsahovať vstupné napätie

(6.5)#\[\begin{split} \begin{align} \begin{split} u_L + u_C &= 0, \\ L \frac{di_L}{dt} + u_C &= 0, \\ L \frac{di_L}{dt} &= -u_C, \\ \frac{di_L}{dt} &= -\frac{1}{L} u_C. \end{split} \end{align} \end{split}\]

Druhá rovnica bude rovnaká ako v prvom intervale činnosti

(6.6)#\[ \begin{align} \frac{du_C}{dt} = \frac{1}{C} i_L - \frac{1}{R \, C} u_C. \end{align} \]

6.1.2. Stavový opis#

Získané diferenciálne rovnice prevedieme do maticového stavu, čím získame kompletný spojitý matematický model znižovacieho meniča

(6.7)#\[ \begin{align} \pmb{\dot{x}} = \pmb{A} \, \pmb{x}+ \pmb{B} \, \pmb{u}. \end{align} \]

Prvý interval činnosti

(6.8)#\[\begin{split} \begin{align} \label{eqn:matrix_notation_b} \frac{\mathrm{d} }{\mathrm{d} t} \begin{pmatrix} i_L \\ u_C \end{pmatrix} = % \begin{pmatrix} 0 & - \frac{1}{L} \\ \frac{1}{C} & -\frac{1}{R \, C} \end{pmatrix} % \begin{pmatrix} i_{L} \\ u_{C} \end{pmatrix} + % \begin{pmatrix} \frac{1}{L} & 0 \\ 0 & 0 \end{pmatrix} % \begin{pmatrix} u_{in} \\ 0 \end{pmatrix}. \end{align} \end{split}\]

Druhý interval činnosti

(6.9)#\[\begin{split} \begin{align} \label{eqn:matrix_notation_c} \frac{\mathrm{d} }{\mathrm{d} t} \begin{pmatrix} i_L \\ u_C \end{pmatrix} = % \begin{pmatrix} 0 & - \frac{1}{L} \\ \frac{1}{C} & -\frac{1}{R \, C} \end{pmatrix} % \begin{pmatrix} i_{L} \\ u_{C} \end{pmatrix} + % \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} % \begin{pmatrix} u_{in} \\ 0 \end{pmatrix}. \end{align} \end{split}\]

6.1.3. Matlab/Octave#

Ukáž kód

% buck converter
clc
close all
clear all

% parametre obvodu
R = 10;
rL = 0.1;
L = 500e-6;
C = 47e-6;

% frekvencia spinania
fs=20e3;

% krok simulacie
dt = 1e-6;
% simulacny cas
Tsim = 20e-3;

% vstupne napatie
us = 100;
% vystupne napatie
uo = 40;

u = [us;0];

% pociatocne podmienky
iL=0;
uC=0;
X=[iL;uC];

% pomerna sirka zopnutia
D=uo/us  

% generovanie piloveho priebehu
t=0:dt:Tsim;
% prva moznost
sawt = 0.5+0.5*sawtooth (2*pi*fs*t , 0.5);
% druha moznost
sawt2 =0.5+0.5*(2/pi)*asin(sin(2*pi*fs*t-pi/2));
% plot(t,sawt, t, sawt2)

n=1;
% nepriama eulerova metoda 
for t=0:dt:Tsim
    % stavove matice
    A1 = [(-rL/L),(-1/L);
          (1/C),(-1/(C*R))];
    B1 = [(1/L),0; 
          0,0];
    
    A2 = [-(rL/L),(-1/L);
          (1/C),(-1/(C*R))];
    B2 = [0,0; 
          0,0];
    
    % jednotkova matica
    E = eye(size(A1));
    
    % matice nepriamej eulerovej metody
    F1 = inv(E-dt*A1);
    G1 = F1*dt*B1;
    
    F2= inv(E-dt*A2);
    G2= F2*dt*B2;
    
    u = [us;0];
    
    % porovnavanie piloveho priebehu
    % s pomernou sirkou zopnutia
    if(sawt(n) < D)           
      X=F1*X+G1*u;
    else          
      X=F2*X+G2*u; 
    end
   
    iL(n)=X(1);
    uC(n)=X(2);
    
    time(n)=t;
    D_graf(n) = D;
   
    % skokova zmena odporu zataze
    if(time(n) > Tsim/2)
       R=1;
    end
     
    n=n+1;
end

% priebehy
subplot(3,1,1)
plot(time(1:1000),sawt(1:1000), time(1:1000), D_graf(1:1000))
xlabel('t [s]');
legend('pila','D');
grid on

subplot(3,1,2)
plot(time,iL)
ylabel('iL [A]');
xlabel('t [s]');
grid on

subplot(3,1,3)
plot(time,uC)
ylabel('uC [V]');
xlabel('t [s]');
grid on

Online simulácia

Spustiť simuláciu

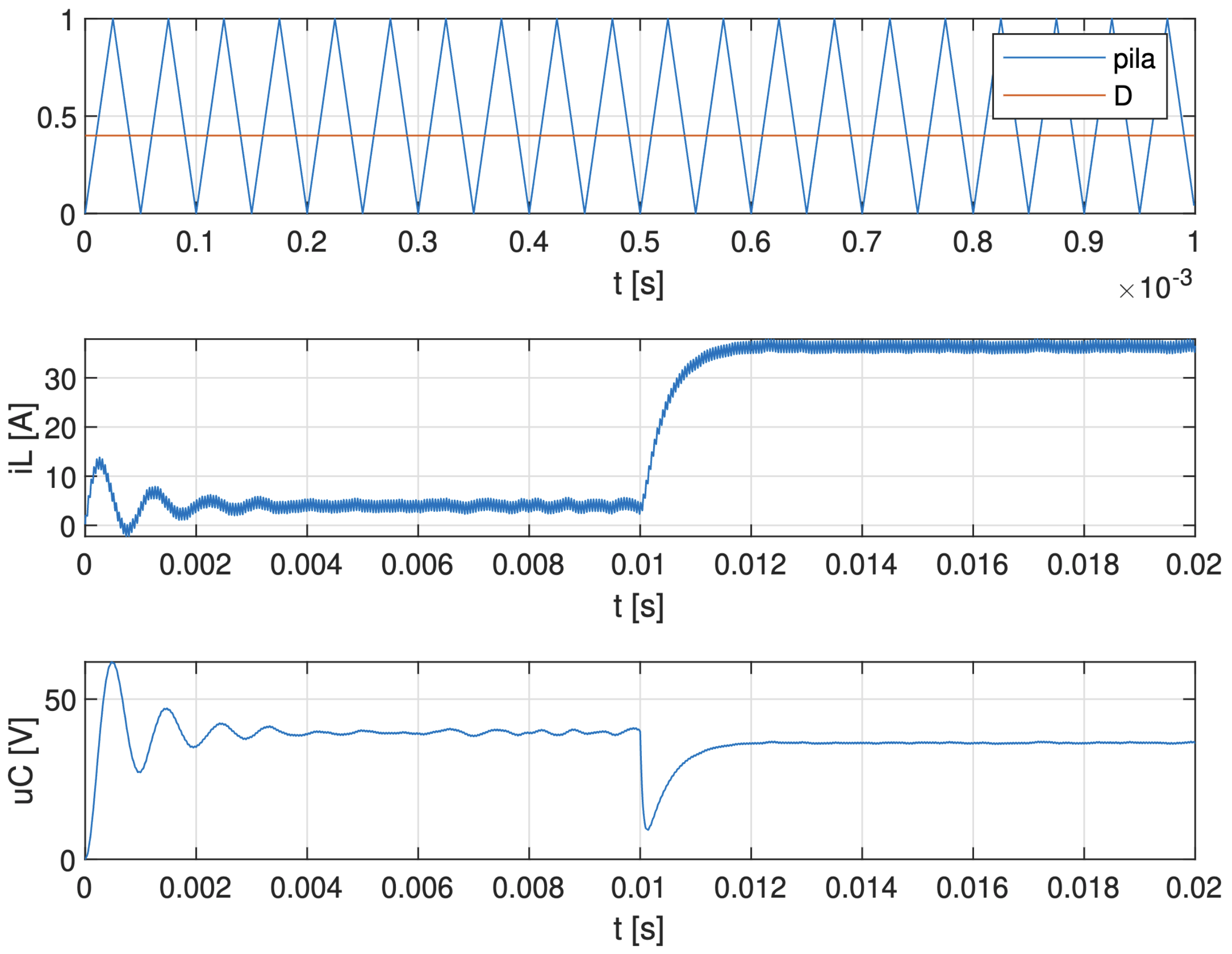
../../../_images/buck.png — Obr. 6.6 Priebehy elektrických veličín znižujúceho meniča.#

6.1.4. Zadanie#

Hore uvedený a analyzovaný príklad znižovacieho Buck meniča bol ideálny t. j. bez statických a dynamických strát, ktoré sa menia na teplo. Na Obr. 6.7. môžeme vidieť model meniča, ktorý uvažuje už aj statické straty v podobe parazitných odporov \(r_Q\), \(r_D\), \(r_L\), \(r_C\). Urobte analýzu tohto buck meniča podobne ako pri ideálnom meniči, získajte diferenciálne rovnice pre oba režimy a rovnice zapíšte v maticovom tvare. Následne vytvorte simuláciu pomocou nepriamej Eulerovej metódy v maticovom tvare v prostredí MATLAB. V určitom čase skokovo zmeňte hodnotu záťaže. Priebehy napätí a prúdov stavových veličín a záťaže zobrazte graficky.

Získané výsledky porovnajte s priebehmi ideálneho meniča. Svoje zistenia a výsledky opíšte v závere.

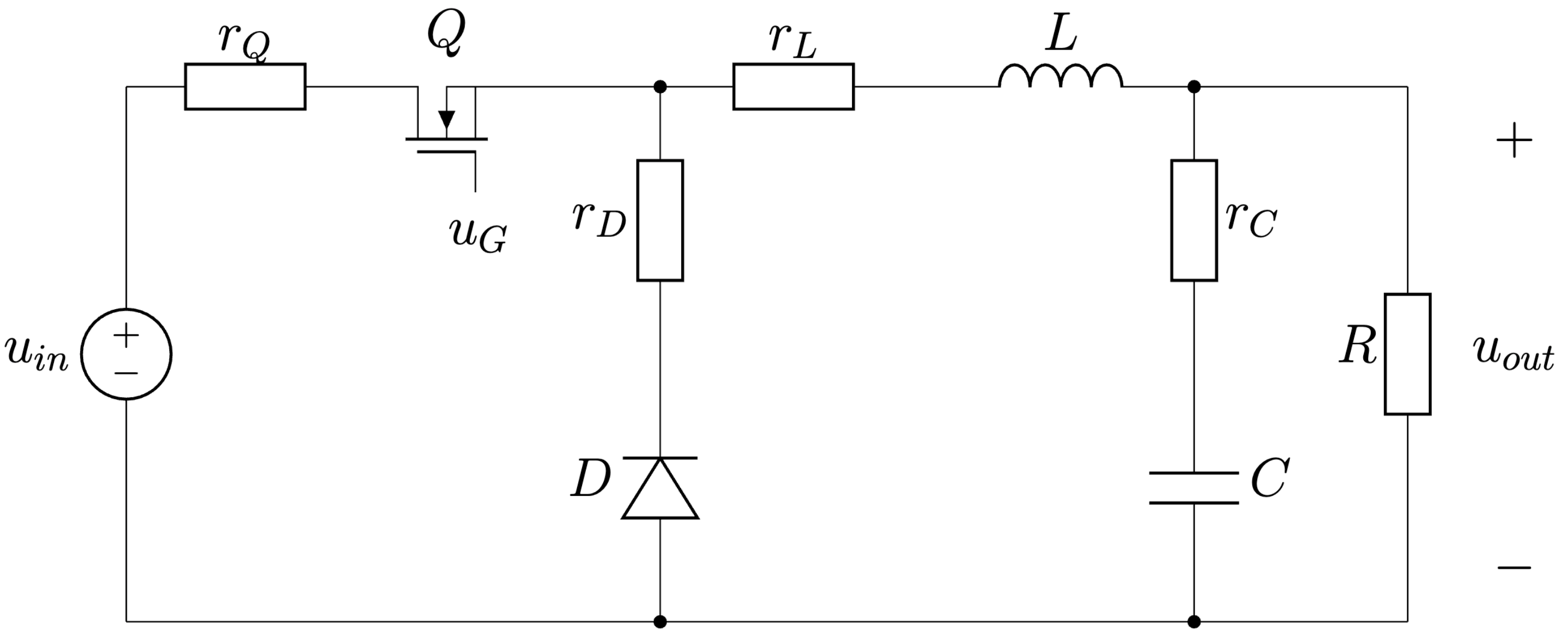
../../../_images/buck_2.png — Obr. 6.7 Znižovací menič (Buck) so statickými stratami.#

Parametre simulácie: \(u_{in} = 30\,\)V, \(u_{out} = 15\) V, \(R = 5 \,\Omega\), \(L = 500 \,\mu\)H, \(C = 47 \,\mu\)F; \(dt = h = 1 \, \mu\)s, \(r_L = 0.5\,\Omega\), \(r_Q = 0.1\,\Omega\), \(r_D = 0.1\,\Omega\), \(r_C = 0.1\,\Omega\), frekvencia spínania \(f = 20\) kHz, skoková zmena záťaže \(R = 1 \,\Omega\) v čase \(t = 10\) ms, celkový čas simulácie 20 ms.

Poznámka: môžete skúsiť meniť hodnoty parazitných odporov, a tým pádom statické straty v meniči. Ak sa nastavia hodnoty parazitných odporov na hodnotu 0, mali by sme dostať rovnaké rovnice ako pri ideálnom meniči. Ďalej môžete skúsiť vyjadriť a zobraziť v grafe účinnosť meniča (nie je povinné).

Nápoveda: Jedna z možností riešenia je použiť iba druhý Kirchhoffov zákon
pre dve slučky v obvode, každá slučka pre jednu diferenciálnu rovnicu. Pomocou substitúcie môžeme nahradiť výstupné napätie ako \(u_{out} = R \, i_R = R(i_L - i_C) = R(i_L - C\frac{du_C}{dt})\). Ak sa v jednej diferenciálnej rovnici vyskytnú obe derivácie \(\frac{du_C}{dt}\) a \(\frac{di_L}{dt}\), dosadíme druhú diferenciálnu rovnicu do prvej, aby sme sa zbavili druhej derivácie. Máme dve stavové veličiny \(i_L\) a \(u_c\) a preto potrebujeme dve diferenciálne rovnice prvého rádu \(\frac{di_L}{dt} = f_1(...)\) a \(\frac{du_C}{dt} = f_2(...)\) pri jednom režime spínania.