2.2. Kirchhoffove zákony#
Kirchhoffove zákony predstavujú dva významné vzťahy, ktoré sa týkajú prúdov a napätí v elektrických obvodoch a sú pomenované po ich objaviteľovi, Gustavovi Robertovi Kirchhoffovi. Tieto zákony patria k základným nástrojom pre analýzu elektrických a elektronických obvodov pri použití modelu prvkov so sústredenými parametrami. Tieto zákony platia pre jednosmerné, striedavé, konštantné a časovo sa meniace veličiny. Oba zákony možno odvodiť aj z Maxwellových rovníc.
2.2.1. Prvý Kirchhoffov zákon#
Prvý Kirchhoffov zákon hovorí, že pre akýkoľvek uzol v elektrickom obvode platí, že súčet prúdov vstupujúcich do uzla sa rovná súčtu prúdov z uzla vystupujúcich, Obr. 2.1 . Môžeme ho formulovať aj tak, že algebrický súčet všetkých prúdov v uzle sa rovná nule. Tento princíp môžeme vyjadriť ako
kde \(n\) je počet prúdov v uzle a \(k\) je index prúdu.
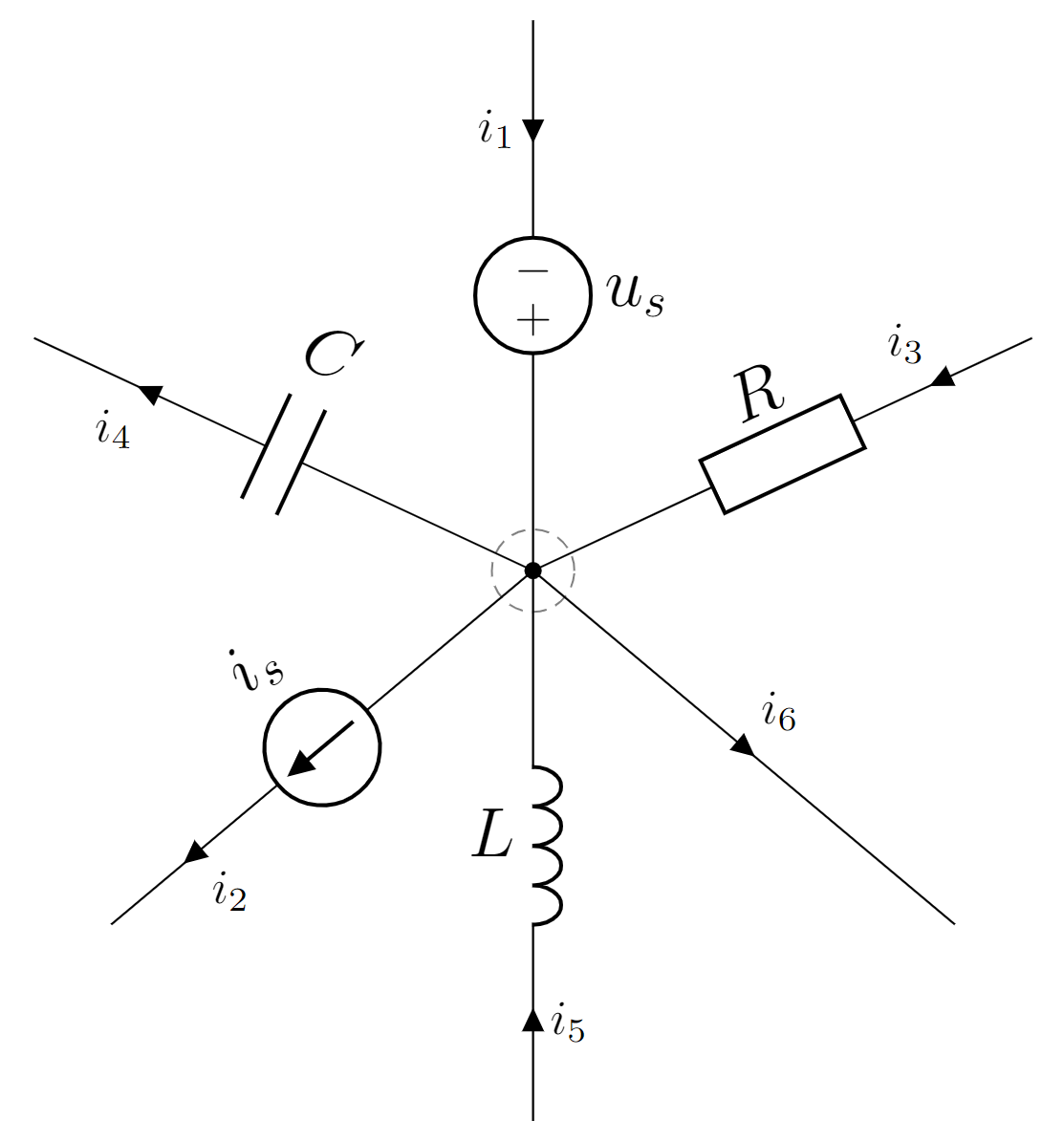
Obr. 2.1 Prvý Kirchhoffov zákon.#
Elektrický prúd je definovaný ako množstvo tečúceho náboja \(Q\) za čas \(t\), preto tento zákon môžeme chápať aj ako rozšírenie zákona zachovania elektrického náboja.
Príklad použitia si ukážeme na Obr. 2.1. Do uzla vstupuje a vystupuje celkovo 6 rôznych prúdov, ktorých súčet sa bude rovnať nule. Môžeme si stanoviť pravidlo, že ak prúdy vstupujú do uzla (smer šípky) majú kladné znamienko, ak vystupujú majú záporné znamienko. Potom algebrická rovnica bude mať tvar
Pravidlo sme si však mohli stanoviť aj naopak. Ak prúdy vstupujú do uzla majú záporné znamienko, ak vystupujú majú kladné znamienko. Rovnica má v tomto prípade tvar
V oboch prípadoch dostaneme rovnaký výsledok.
2.2.2. Druhý Kirchhoffov zákon#
Druhý Kirchhoffov zákon hovorí, že algebrický súčet svorkových napätí (rozdielov elektrických potenciálov) na prvkoch v ľubovoľnej uzavretej slučke elektrického obvodu sa rovná nule, Obr. 2.2. Podobne ako pri predchádzajúcom prípade môžeme zákon vyjadriť pomocou rovnice ako
kde \(n\) je počet napätí v slučke a \(k\) je index napätia.
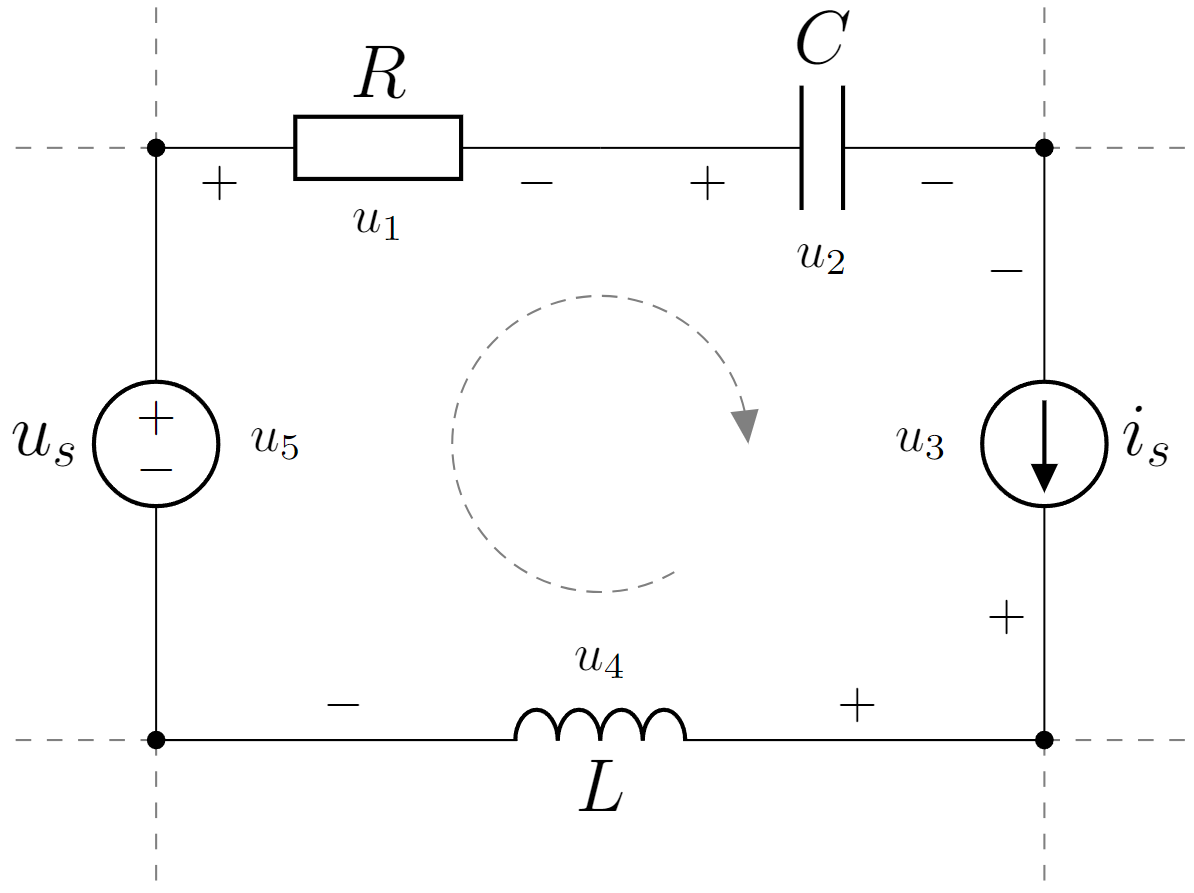
Obr. 2.2 Prvý Kirchhoffov zákon.#
Tento zákon sa zaoberá zachovaním energie v uzavretom obvode. Je to preto, lebo obvodová slučka je uzavretá, takže sa nestráca žiadna energia.
Príklad použitia druhého zákona si ukážeme na Obr. 2.2. V slučke elektrického obvodu je celkovo 5 elektrických prvkov s vyznačenými napätiami a polaritami. Slučka, v ktorej obieha prúd, je vyznačená na obrázku. Aj teraz si môžeme zvoliť pravidlo, závislé na smere prúdu slučky a znamienku napätia na prvku. Pre prípad na obrázku, keď bude prúd v slučke tiecť v smere hodinových ručičiek, bude mať algebrická rovnica tvar
Ak otočíme smer prúdu v slučke, potom bude mať rovnica tvar
Znova dostaneme v oboch prípadoch rovnaký výsledok.