4.1. Úvodný príklad analýzy elektrických obvodov#
V tejto úlohe je zadaný všeobecný príklad s bližšie nešpecifikovanou záťažou, ktorej parametre nie sú jednoznačne určené. Z tohoto dôvodu nám táto záťaž figuruje ako “neznáma” veličina, a preto ju budeme považovať za vstupnú funkciu (budiacu veličinu).
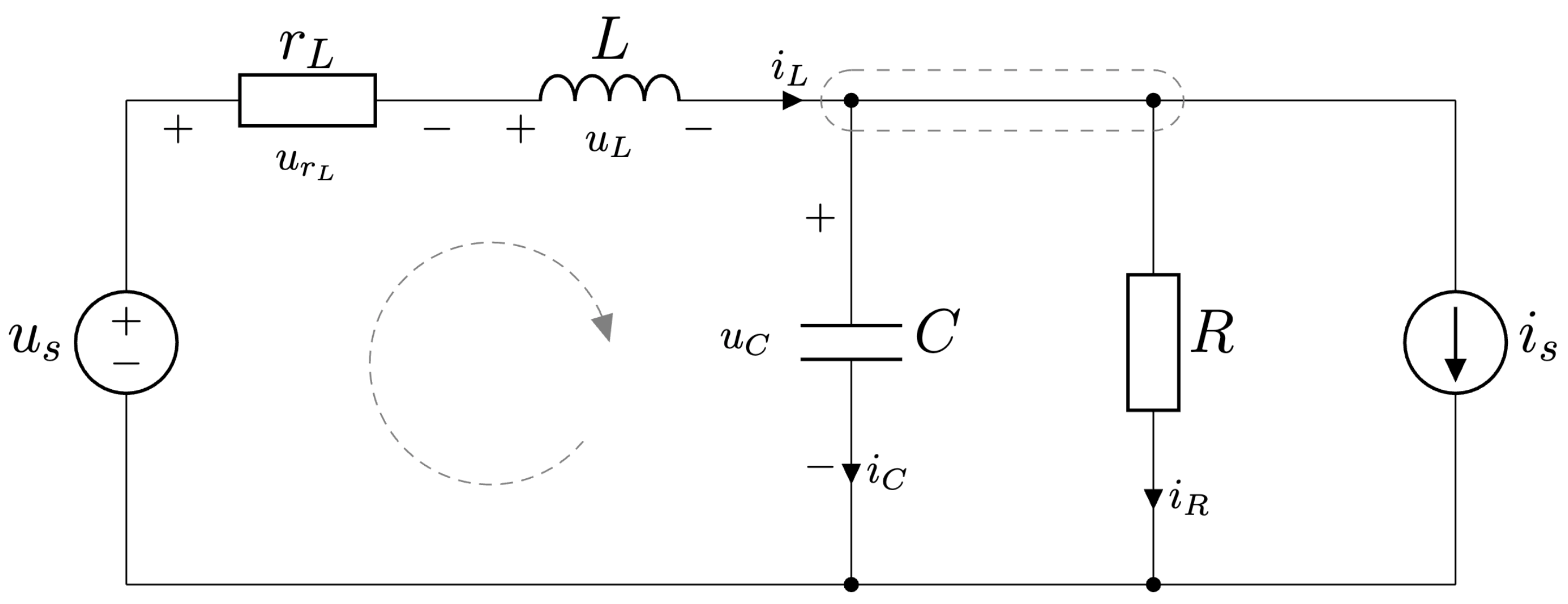
Obr. 4.1 Elektrický obvod.#
Na získanie prvej diferenciálnej rovnice najskôr použijeme druhý Kirchhoffov zákon
(4.1)#\[\begin{split}
\begin{align} %\label{eqn:diff_system1}
\begin{split}
-u_{s} + u_{r_L}+u_L + u_C &= 0, \\
-u_{s} + r_L \, i_L+L \frac{\mathrm{d} i_L}{\mathrm{d} t} + u_C &= 0, \\
L \frac{\mathrm{d} i_L}{\mathrm{d} t} &= -r_L \, i_L-u_C + u_{s}, \\
\frac{\mathrm{d} i_L}{\mathrm{d} t} &= -\frac{r_L}{L}\, i_L-\frac{1}{L} u_C + \frac{1}{L} u_{s}.
\end{split}
\end{align}
\end{split}\]
Ďalej použijeme prvý Kirchhoffov zákon na získanie druhej diferenciálnej rovnice
(4.2)#\[\begin{split}
\begin{align} %\label{eqn:diff_system1}
\begin{split}
-i_L +i_C +i_R+i_s &= 0, \\
-i_L + C \frac{\mathrm{d} u_C}{dt} + \frac{1}{R} u_C + i_s &= 0, \\
C \frac{\mathrm{d} u_C}{\mathrm{d} t} &= i_L - \frac{1}{R} u_C - i_s, \\
\frac{\mathrm{d} u_C}{\mathrm{d} t} &= \frac{1}{C} i_L - \frac{1}{R \, C} u_C - \frac{1}{C} i_s.
\end{split}
\end{align}
\end{split}\]
4.1.1. Stavový opis#
Získané diferenciálne rovnice prevedieme do maticového stavu čím získame spojitý stavový model systému.
(4.3)#\[\begin{split}
\begin{align}
\begin{split}
\frac{\mathrm{d} i_L}{\mathrm{d} t} &= -\frac{r_L}{L}\, i_L-\frac{1}{L} u_C + \frac{1}{L} u_{s}, \\
\frac{\mathrm{d} u_C}{\mathrm{d} t} &= \frac{1}{C} i_L - \frac{1}{R \, C} u_C - \frac{1}{C} i_s.
\end{split}
\end{align}
\end{split}\]
(4.4)#\[
\begin{align}
\pmb{\dot{x}} = \frac{\mathrm{d} \, \pmb{x}}{\mathrm{d} t}=\pmb{A} \, \pmb{x}+ \pmb{B} \, \pmb{u},
\end{align}
\]
(4.5)#\[\begin{split}
\begin{align}
\frac{\mathrm{d} }{\mathrm{d} t}
\begin{pmatrix}
i_L \\
u_C
\end{pmatrix} =
%
\begin{pmatrix}
-\frac{r_L}{L} & - \frac{1}{L} \\
\frac{1}{C} & -\frac{1}{R \, C}
\end{pmatrix}
%
\begin{pmatrix}
i_{L} \\ u_{C}
\end{pmatrix} +
%
\begin{pmatrix}
\frac{1}{L} & 0 \\ 0 & -\frac{1}{C}
\end{pmatrix}
%
\begin{pmatrix}
u_{s} \\ i_s
\end{pmatrix}.
\end{align}
\end{split}\]
(4.6)#\[\begin{split}
\begin{align}
\pmb{x} = \begin{pmatrix}
i_L \\
u_C
\end{pmatrix}, \,
\pmb{u} = \begin{pmatrix}
u_{s} \\ i_s
\end{pmatrix}, \,
\pmb{A} = \begin{pmatrix}
-\frac{r_L}{L} & - \frac{1}{L} \\
\frac{1}{C} & -\frac{1}{R \, C}
\end{pmatrix}, \,
\pmb{B} = \begin{pmatrix}
\frac{1}{L} & 0 \\ 0 & -\frac{1}{C}
\end{pmatrix}.
\end{align}
\end{split}\]