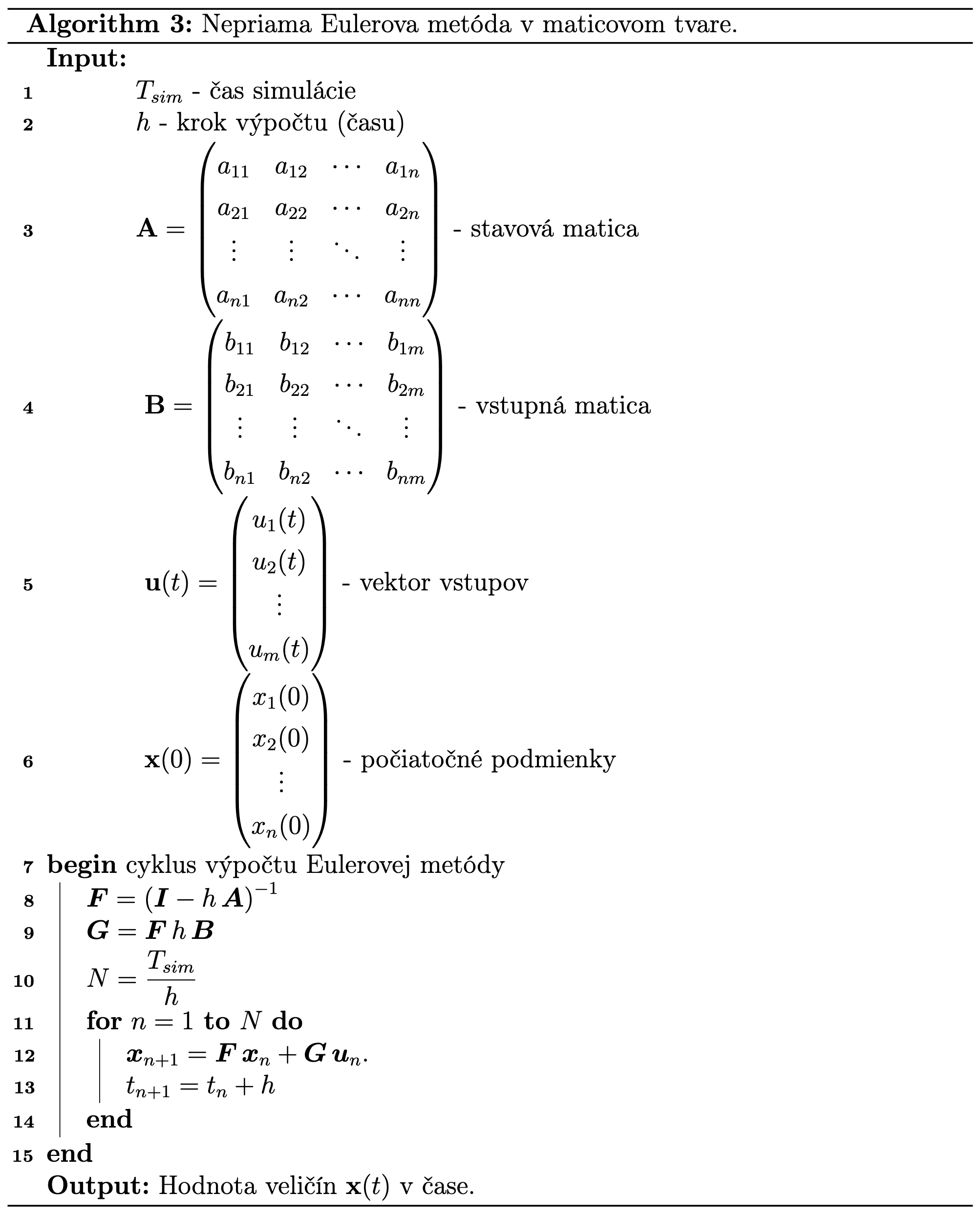
3.5. Použitie nepriamej Eulerovej metódy na riešenie lineárneho systémuRovnako ako pri priamej Eulerovej metóde, aj pri nepriamej Eulerovej metóde môžeme odvodiť vzťah v maticovom tvare. Vychádzame znova z rovníc pre opis lineárneho dynamického systému (3.16) a rovnice nepriamej Eulerovej metódy (3.41) .
(3.47) \[
\begin{align}
\frac{\mathrm{d} \mathbf{x}(t)}{ \mathrm{d}t} \thickapprox \frac{ \mathbf{x}_{n+1}-\mathbf{x}_{n}}{h} = \mathbf{A} \, \mathbf{x}_{n+1} + \mathbf{B} \, \mathbf{u}_{n+1}
\end{align}
\]
Znova použijeme vhodné matematické úpravy, ktoré nás povedú k výslednej rovnici
(3.48) \[\begin{split}
\begin{align}
\begin{split}
\mathbf{x}_{n+1} - \mathbf{x}_n &= h \, \left( \mathbf{A} \, \mathbf{x}_{n+1} + \mathbf{B} \, \mathbf{u}_{n+1} \right) \\
\mathbf{x}_{n+1} &=\mathbf{x}_n + h \, \left( \mathbf{A} \, \mathbf{x}_{n+1} + \mathbf{B} \, \mathbf{u}_{n+1} \right) \\
\mathbf{x}_{n+1} &=\mathbf{x}_n + h \, \mathbf{A} \, \mathbf{x}_{n+1} + h \,\mathbf{B} \, \mathbf{u}_{n+1} \\
\mathbf{x}_{n+1} - h \, \mathbf{A} \, \mathbf{x}_{n+1} &=\mathbf{x}_n + h \, \mathbf{B} \, \mathbf{u}_{n+1} \\
\left(\mathbf{I} - h \, \mathbf{A}\right) \, \mathbf{x}_{n+1} &= \mathbf{x}_n + h \, \mathbf{B}\, \mathbf{u}_{n+1}.
\end{split}
\end{align}
\end{split}\]
Potom platí
(3.49) \[
\begin{align}
\mathbf{x}_{n+1} &= \left(\mathbf{I} - h \, \mathbf{A}\right)^{-1}\, \mathbf{x}_n + \left(\mathbf{I} - h \, \mathbf{A}\right)^{-1} \,h \, \mathbf{B}\, \mathbf{u}_{n+1}
\end{align}
\]
Tento vzťah môžeme ďalej zjednodušiť substitúciou
(3.50) \[
\begin{align}
\mathbf{x}_{n+1} &= \underbrace{\left(\mathbf{I} - h \, \mathbf{A}\right)^{-1}}_{\mathbf{F}}\, \mathbf{x}_n + \underbrace{\left(\mathbf{I} - h \, \mathbf{A}\right)^{-1} \,h \, \mathbf{B}}_{\mathbf{G}}\, \mathbf{u}_{n+1}
\end{align}
\]
Definujeme maticu \(\mathbf{F}\) ako,
(3.51) \[
\begin{align}
\mathbf{F} = \left(\mathbf{I} - h \, \mathbf{A}\right)^{-1}
\end{align}
\]
a maticu \(\mathbf{G}\) ako,
(3.52) \[
\begin{align}
\mathbf{G} = \left(\mathbf{I} - h \, \mathbf{A}\right)^{-1} \,h \, \mathbf{B} = \mathbf{F} \, h \, \mathbf{B}.
\end{align}
\]
Nepriama Eulerová metóda pre lineárny dynamický systém v maticovom tvare bude potom daná vzťahom
(3.53) \[
\begin{align}
\mathbf{x}_{n+1} = \mathbf{F} \, \mathbf{x}_n + \mathbf{G} \, \mathbf{u}_{n+1}
\end{align}
\]
Tým sme znova úspešne odvodili vzorec nepriamej Eulerovej metódy pre lineárny systém v maticovom tvare. Ako už bolo spomínané vyššie, na rozdiel od priamej metódy však nebude mať problém so stabilitou konvergencie.