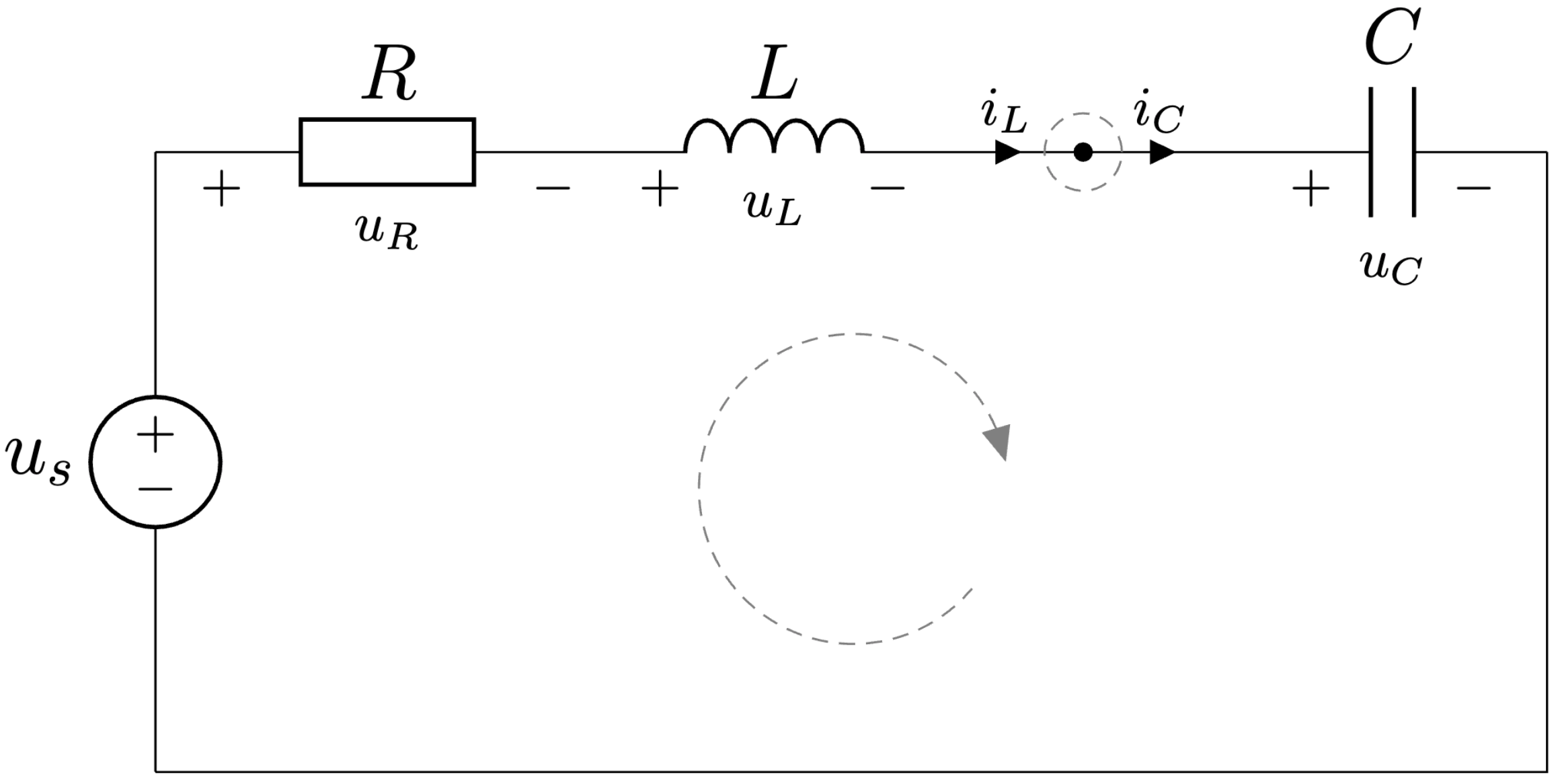
4.3. Sériový RLC obvod#

Sériový RLC obvod, alebo sériový RLC rezonančný obvod je obvod, ktorého správanie je závislé od parametrov obvodu, predovšetkým od činiteľa tlmenia. Budiacou veličinou sériového rezonančného obvodu je napäťový napájací zdroj.

../../../_images/series_rlc_circuit.png

Obr. 4.4 Sériový RLC obvod.#

Na získanie prvej diferenciálnej rovnice najskôr použijeme druhý Kirchhoffov zákon

(4.14)#\[\begin{split} \begin{align} \begin{split} -u_{s} + u_{R}+u_L + u_C &= 0, \\ -u_{s} + R \, i_L+L \frac{di_L}{dt} + u_C &= 0, \\ L \frac{di_L}{dt} &= -R \, i_L-u_C + u_{s}, \\ \frac{di_L}{dt} &= -\frac{R}{L}\, i_L-\frac{1}{L} u_C + \frac{1}{L} u_{s}. \end{split} \end{align} \end{split}\]

Ďalej použijeme prvý Kirchhoffov zákon na získanie druhej diferenciálnej rovnice

(4.15)#\[\begin{split} \begin{align} \begin{split} -i_C +i_{L} &= 0, \\ -C \frac{du_C}{dt} + i_L &= 0, \\ C \frac{du_C}{dt} &= i_L, \\ \frac{du_C}{dt} &= \frac{1}{C} i_L. \end{split} \end{align} \end{split}\]

4.3.1. Stavový opis#

Získané diferenciálne rovnice prevedieme do maticového stavu

(4.16)#\[\begin{split} \begin{align} \begin{split} \frac{di_L}{dt} &= -\frac{R}{L}\, i_L-\frac{1}{L} u_C + \frac{1}{L} u_{s}, \\ \frac{du_C}{dt} &= \frac{1}{C} i_L. \end{split} \end{align} \end{split}\]
(4.17)#\[ \begin{align} \pmb{\dot{x}} = \frac{\mathrm{d} \, \pmb{x}}{\mathrm{d} t}=\pmb{A} \, \pmb{x}+ \pmb{B} \, \pmb{u}, \end{align} \]
(4.18)#\[\begin{split} \begin{align} \frac{\mathrm{d} }{\mathrm{d} t} \begin{pmatrix} i_L \\ u_C \end{pmatrix} = % \begin{pmatrix} -\frac{R}{L} & - \frac{1}{L} \\ \frac{1}{C} & 0 \end{pmatrix} % \begin{pmatrix} i_{L} \\ u_{C} \end{pmatrix} + % \begin{pmatrix} \frac{1}{L} \\ 0 \end{pmatrix} % u_{s} . \end{align} \end{split}\]
(4.19)#\[\begin{split} \begin{align} \pmb{x} = \begin{pmatrix} i_L \\ u_C \end{pmatrix}, \, \pmb{u} = u_{s}, \, \pmb{A} = \begin{pmatrix} -\frac{R}{L} & - \frac{1}{L} \\ \frac{1}{C} & 0 \end{pmatrix}, \, \pmb{B} = \begin{pmatrix} \frac{1}{L} \\ 0 \end{pmatrix}. \end{align} \end{split}\]

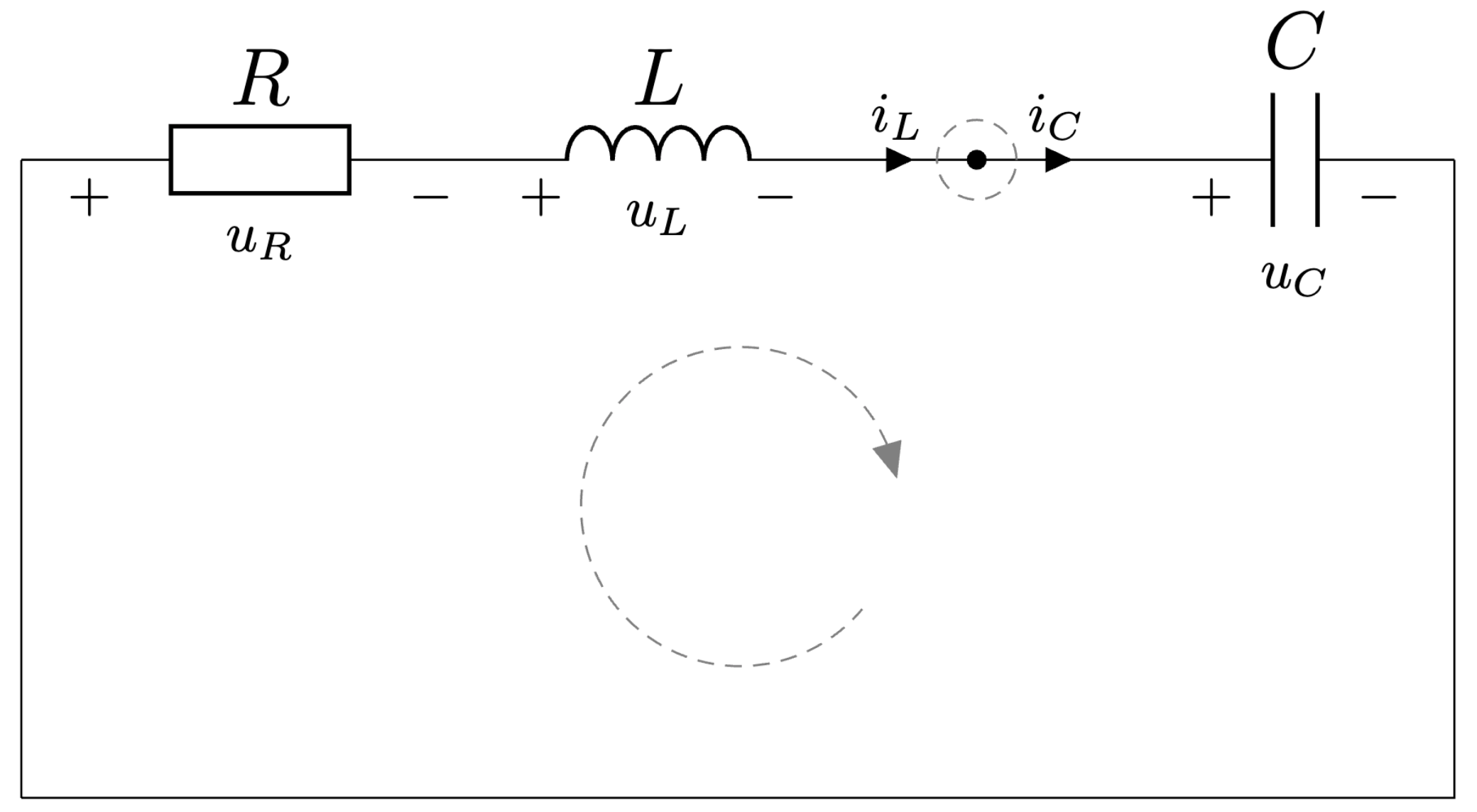
4.3.2. Sériový RLC obvod bez vonkajšieho budenia#

V tomto type sériového rezonančného obvodu je zdrojom energie jeden, alebo oba akumulačné prvky (L, C), ktorých počiatočná energia bude budiť obvod.

../../../_images/series_rlc_circuit_2.png

Obr. 4.5 Sériový RLC obvod bez vonkajšieho budenia.#

Najprv použijeme druhý Kirchhoffov zákon na získanie prvej diferenciálnej rovnice

(4.20)#\[\begin{split} \begin{align} \begin{split} u_{R}+u_L + u_C &= 0, \\ R \, i_L+L \frac{di_L}{dt} + u_C &= 0, \\ L \frac{di_L}{dt} &= -R \, i_L-u_C , \\ \frac{di_L}{dt} &= -\frac{R}{L}\, i_L-\frac{1}{L} u_C. \end{split} \end{align} \end{split}\]

Ďalej použijeme prvý Kirchhoffov zákon na získanie druhej diferenciálnej rovnice

(4.21)#\[\begin{split} \begin{align} \label{eqn:diff_system1d} \begin{split} -i_C +i_{L} &= 0, \\ -C \frac{du_C}{dt} + i_L &= 0, \\ C \frac{du_C}{dt} &= i_L, \\ \frac{du_C}{dt} &= \frac{1}{C} i_L. \end{split} \end{align} \end{split}\]

4.3.3. Stavový opis#

Získané diferenciálne rovnice prevedieme do maticového stavu

(4.22)#\[\begin{split} \begin{align} \begin{split} \frac{di_L}{dt} &= -\frac{R}{L}\, i_L-\frac{1}{L} u_C, \\ \frac{du_C}{dt} &= \frac{1}{C} i_L. \end{split} \end{align} \end{split}\]
(4.23)#\[ \begin{align} \label{eqn:_matrix_notation_c} \pmb{\dot{x}} = \frac{\mathrm{d} \, \pmb{x}}{\mathrm{d} t}=\pmb{A} \, \pmb{x}+ \pmb{B} \, \pmb{u}, \end{align} \]
(4.24)#\[\begin{split} \begin{align} \frac{\mathrm{d} }{\mathrm{d} t} \begin{pmatrix} i_L \\ u_C \end{pmatrix} = % \begin{pmatrix} -\frac{R}{L} & - \frac{1}{L} \\ \frac{1}{C} & 0 \end{pmatrix} % \begin{pmatrix} i_{L} \\ u_{C} \end{pmatrix}. \end{align} \end{split}\]
(4.25)#\[\begin{split} \begin{align} \pmb{x} = \begin{pmatrix} i_L \\ u_C \end{pmatrix}, \, \pmb{A} = \begin{pmatrix} -\frac{R}{L} & - \frac{1}{L} \\ \frac{1}{C} & 0 \end{pmatrix}. \end{align} \end{split}\]

4.3.4. Matlab/Octave#

Ukáž kód

% seriovy RLC obvod
clc
clear all
close all

% parametre obvodu
us=100;
L=1e-3;
C=1e-3;
R=0;
% krok simulacie
dt=1e-6;
% simulacny cas
Tsim=100e-3;

u=[us;0];

% pociatocne podmienky
iL=0;
uC=0;
x=[iL;uC];

n=1;
% nepriama eulerova metoda 
for t = 0:dt:Tsim
    % stavove matice
    A=[-R/L  -1/L;
    1/C    0];

    B=[1/L  0;
        0   0];

    % matice nepriamej eulerovej metody
    F=inv(eye(size(A))-dt*A);
    G=F*dt*B;

    x=F*x+G*u;
    iL(n)=x(1);
    uC(n)=x(2);
    time(n)=t;
    n=n+1;
    %skokova zmena odporu
    if t > Tsim/2
        R = 0.2;
    end
end

uL = us-R*iL-uC;
uR = R*iL;

% priebehy
figure 
subplot(4,1,1)
plot(time,uC)
ylabel('uC [V]');
xlabel('t [s]');
grid on

subplot(4,1,2)
plot(time,iL)
ylabel('iL [A]');
xlabel('t [s]');
grid on

subplot(4,1,3)
plot(time, uL)
ylabel('uL [V]');
xlabel('t [s]');
grid on

subplot(4,1,4)
plot(time, uR),grid
ylabel('uR [V]');
xlabel('t [s]');
grid on

Online simulácia

Spustiť simuláciu

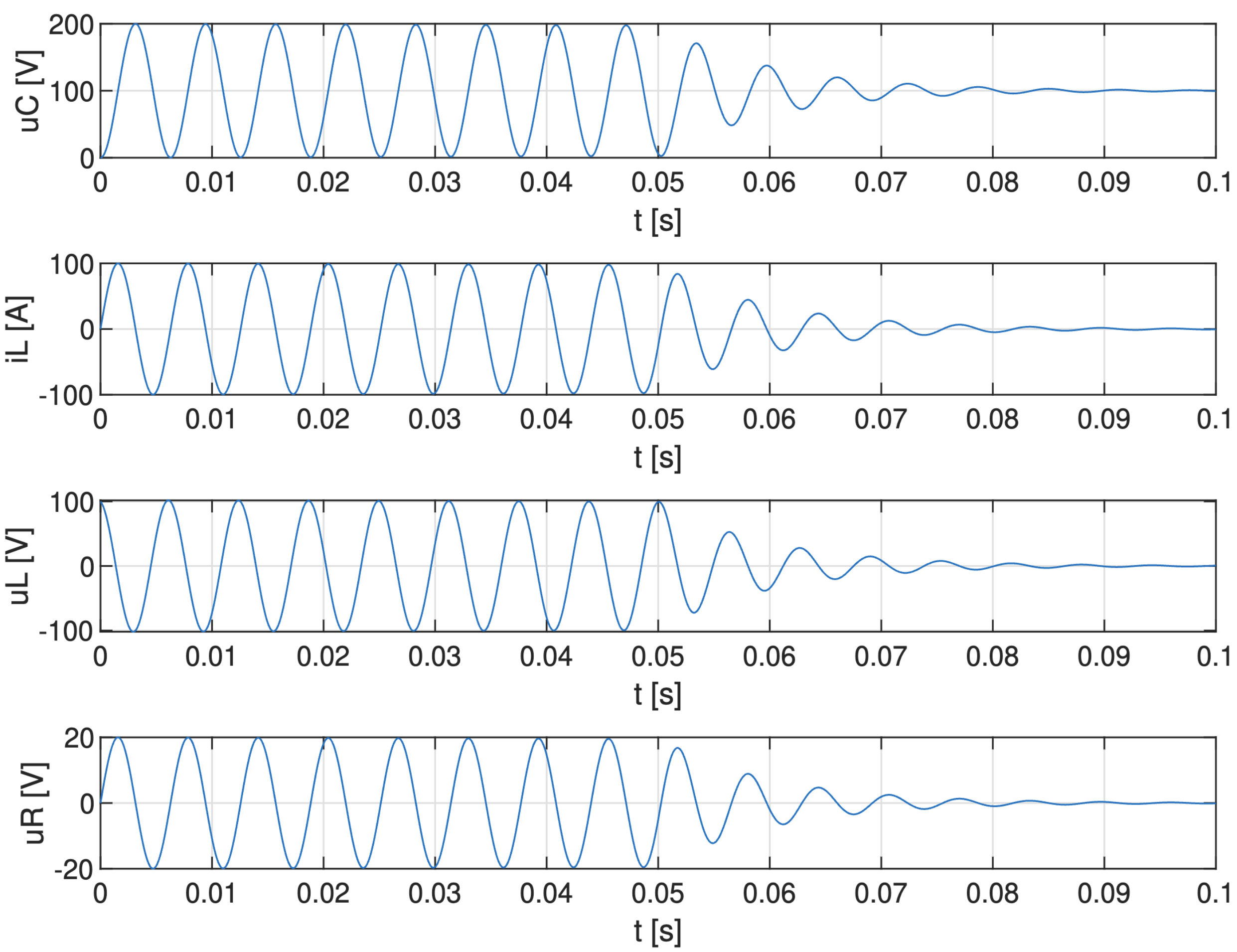
../../../_images/serial_rlc.png

Obr. 4.6 Priebehy elektrických veličín sériového RLC obvodu.#