6.3. Invertujúci DC/DC menič (Buck-boost)#

Ďalším často používaným spínaným zdrojom je invertujúci DC/DC menič (buck-boost), Obr. 6.15. Jeho výstupné napätie môže byť väčšie alebo menšie, ako jeho vstupné napätie a výstupné napätie má opačnú polaritu ako je na vstupe. Toto môže predstavovať nevýhodu pre použitie v niektorých aplikáciách, keďže tento typ meniča nemá galvanickú izoláciu medzi vstupom a výstupom.

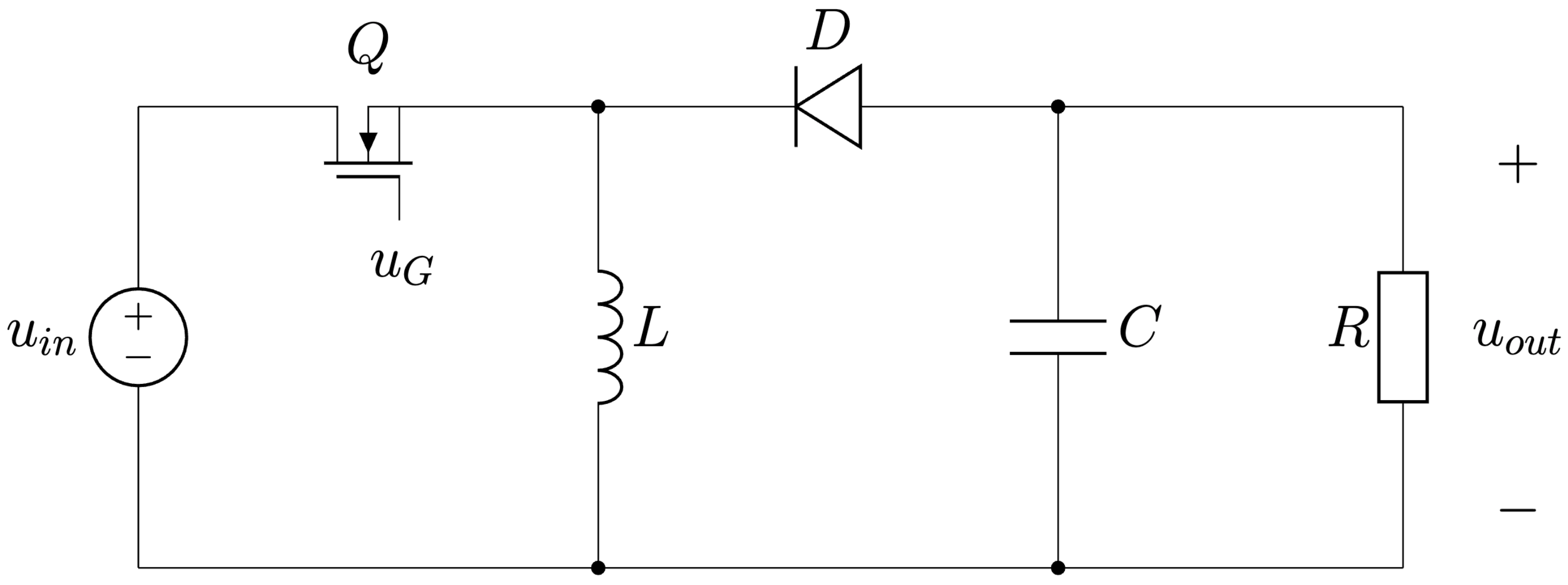
../../../_images/buck_boost.png

Obr. 6.15 Invertujúci menič (Buck-Boost).#

Princíp činnosti tohoto meniča, s použitím náhrady v podobe dvojpolohového spínača, je zobrazený na Obr. 6.16. V polohe spínača 1 (tranzistor zopnutý, dióda rozopnutá - záverný smer) sa energia zo vstupu akumuluje v cievke \(L\) (pracuje ako spotrebič) a energia do záťaže je dodávaná len z kondenzátora \(C\). V polohe spínača 2 (tranzistor rozopnutý, dióda zopnutá - priepustný smer ) je energia dodávaná z cievky \(L\) (pracuje ako zdroj) do kondenzátora \(C\) a záťaže \(R\).

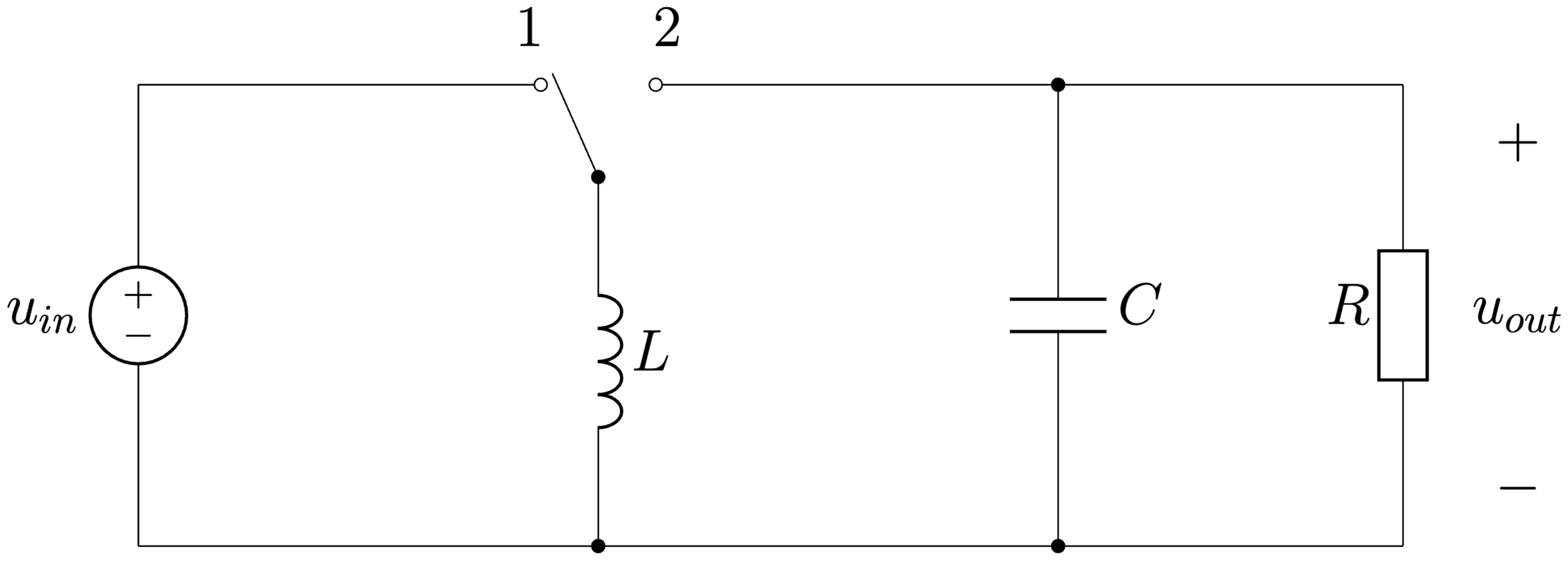
../../../_images/buck_boost_sw.png

Obr. 6.16 Principiálne fungovanie invertujúceho meniča s dvojpolohovým spínačom.#

Prevodová charakteristika medzi vstupným a výstupný napätím ideálneho invertujúceho meniča je zobrazená na Obr. 6.17.

Hodnota výstupného napätia je daná nasledujúcim vzťahom

(6.18)#\[ \begin{align} \label{eqn:uout_bb} u_{out} = \dfrac{-D}{1-D} \, u_{in}, \end{align} \]

kde \(u_{in}\) je vstupné napätie, \(u_{out}\) je výstupné napätie a \(D\) je pomerná širka zopnutia (strieda) PWM signálu spínača v polohe 1.

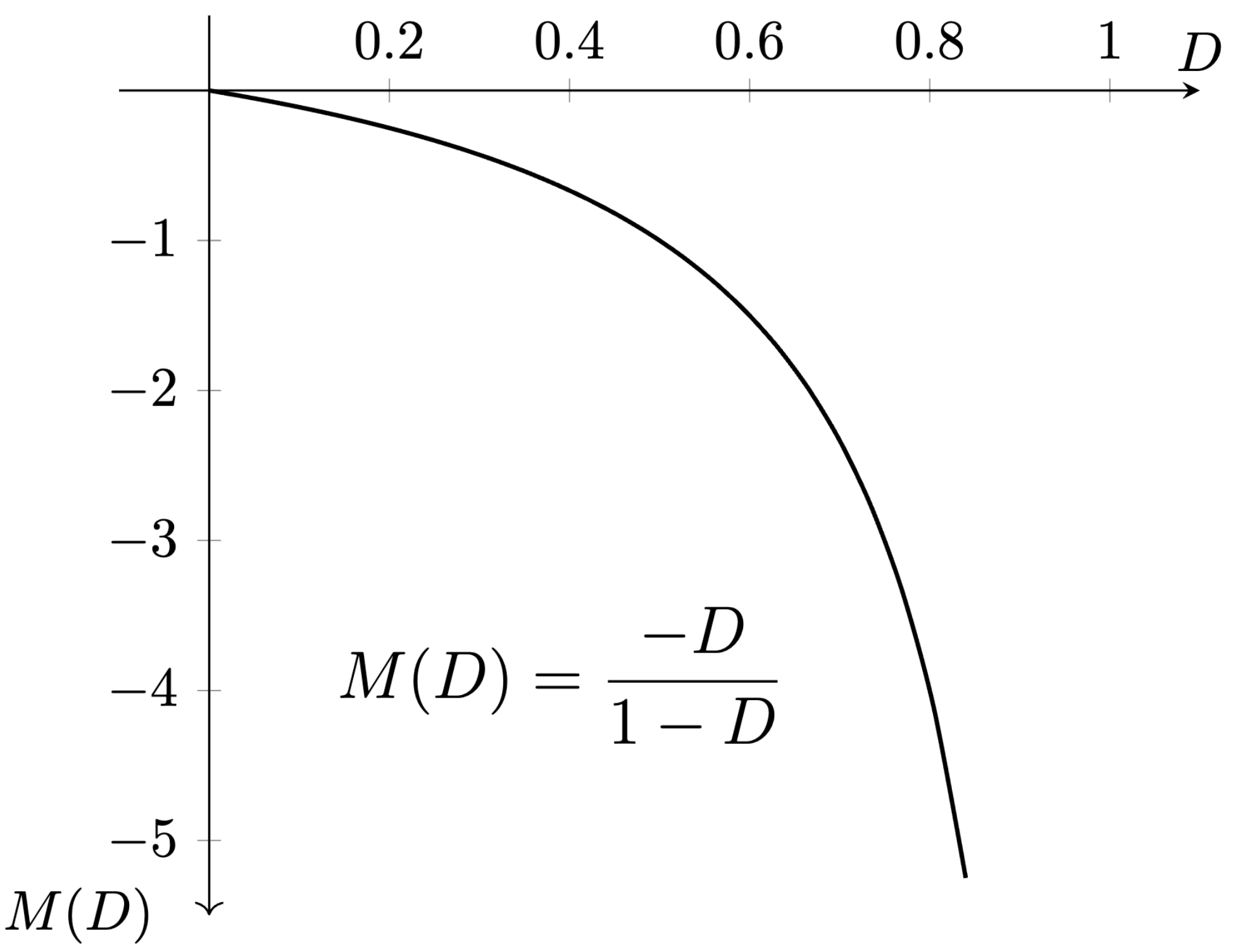
../../../_images/buck_boost_conversion.png

Obr. 6.17 Prevodová charakteristika medzi vstupným a výstupný napätím ideálneho invertujúceho meniča.#

Ako je vidieť z grafu, najvyššie napätie aké môžeme dostať na výstupe je 0 voltov, najnižšie napätie je teoreticky u ideálneho meniča záporných nekonečne voltov, v skutočnosti pri reálnom meniči to tak samozrejme nie je v dôsledku strát meniča.

6.3.1. Prvý interval činnosti#

Topológia meniča pre prvý interval činnosti je zobrazená na Obr. 6.18.

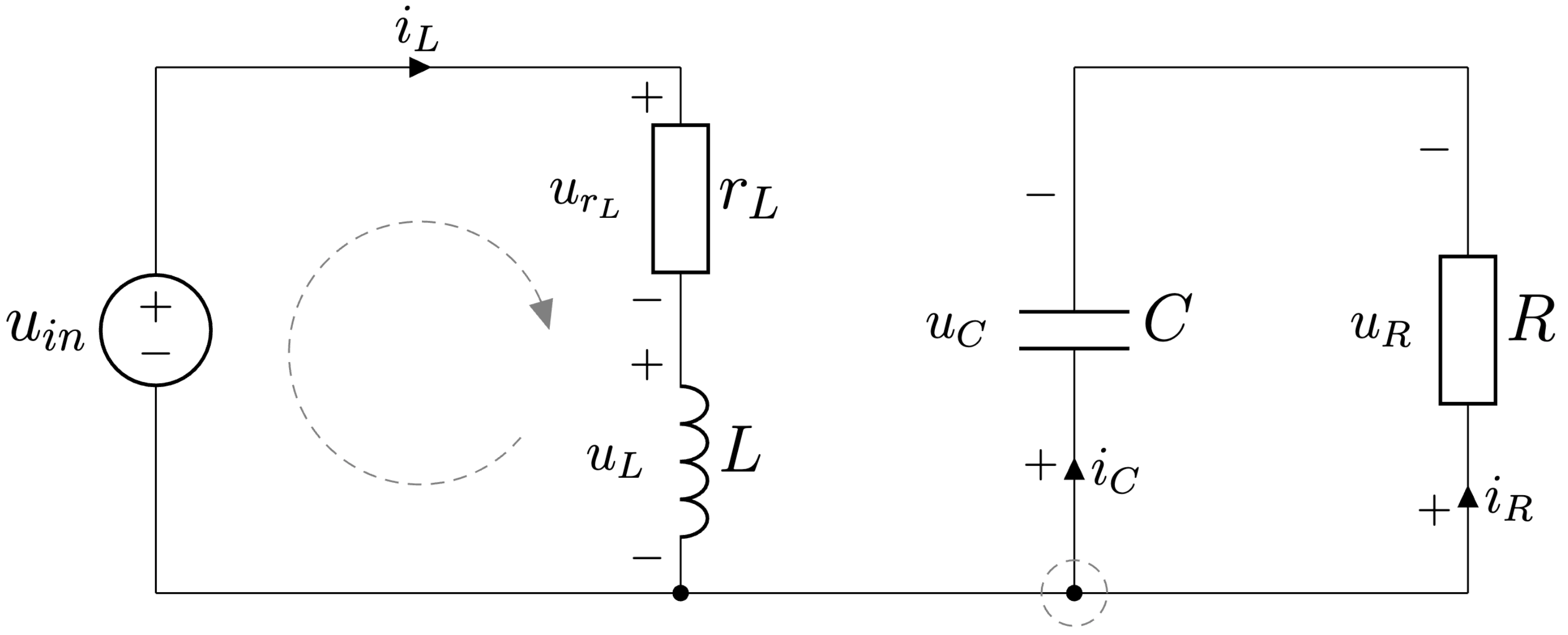
../../../_images/buck_boost_state_1.png

Obr. 6.18 Invertujúci menič - prvý interval činnosti.#

Najprv použijeme druhý Kirchhoffov zákon na získanie prvej diferenciálnej rovnice

(6.19)#\[\begin{split} \begin{align} \begin{split} -u_{in} + u_{r_L} + u_L &= 0, \\ -u_{in} + r_L \, i_L +L \frac{di_L}{dt} &= 0, \\ L \frac{di_L}{dt} &= -r_L \, i_L + u_{in}, \\ \frac{di_L}{dt} &= -\frac{r_L}{L} \, i_L + \frac{1}{L} u_{in}. \end{split} \end{align} \end{split}\]

Ďalej použijeme prvý Kirchhoffov zákon na získanie druhej diferenciálnej rovnice

(6.20)#\[\begin{split} \begin{align} \begin{split} -i_C-i_R &= 0, \\ - C \frac{du_C}{dt} - \frac{1}{R} u_C &= 0, \\ - C \frac{du_C}{dt} &= \frac{1}{R} u_C, \\ \frac{du_C}{dt} &= - \frac{1}{R \, C} u_C. \end{split} \end{align} \end{split}\]

6.3.2. Druhý interval činnosti#

Topológia meniča pre druhý interval činnosti je zobrazená na Obr. 6.19.

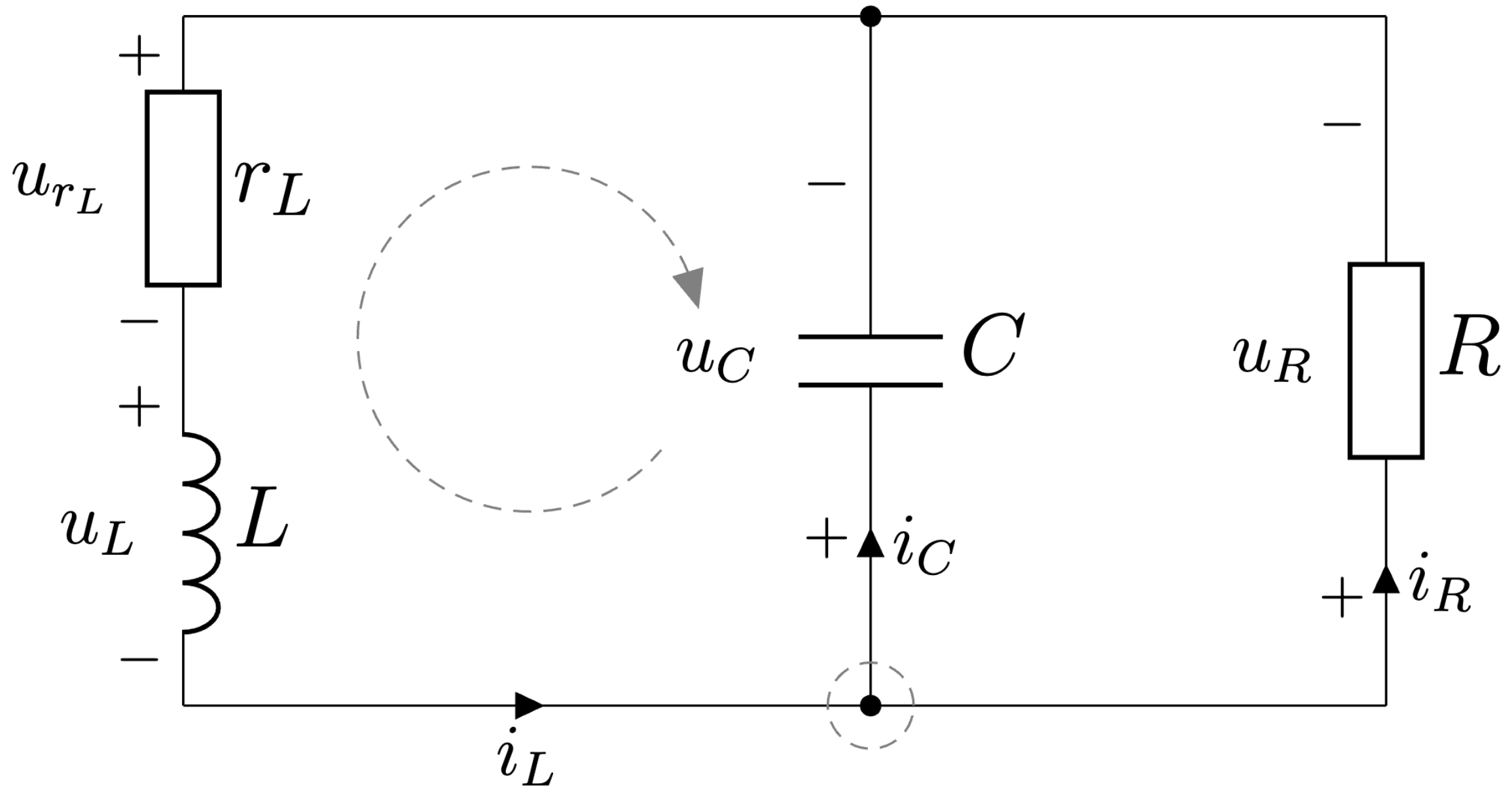
../../../_images/buck_boost_state_2.png

Obr. 6.19 Invertujúci menič - druhý interval činnosti.#

Najprv použijeme druhý Kirchhoffov zákon na získanie prvej diferenciálnej rovnice

(6.21)#\[\begin{split} \begin{align} \begin{split} -u_L - u_{r_L} - u_C &= 0, \\ -L \frac{di_L}{dt} - r_L \, i_L - u_C &= 0, \\ -L \frac{di_L}{dt} &= r_L \, i_L + u_C, \\ \frac{di_L}{dt} &= -\frac{r_L}{L} \, i_L -\frac{1}{L} u_C. \end{split} \end{align} \end{split}\]

Ďalej použijeme prvý Kirchhoffov zákon na získanie druhej diferenciálnej rovnice

(6.22)#\[\begin{split} \begin{align} \begin{split} i_L - i_C - i_R &= 0, \\ i_L - C \frac{du_C}{dt} - \frac{1}{R} u_C &= 0, \\ - C \frac{du_C}{dt} &= -i_L + \frac{1}{R} u_C, \\ \frac{du_C}{dt} &= \frac{1}{C} i_L - \frac{1}{R \, C} u_C. \end{split} \end{align} \end{split}\]

6.3.3. Stavový opis#

Získané diferenciálne rovnice prevedieme do maticového stavu

(6.23)#\[ \begin{align} \pmb{\dot{x}} = \pmb{A} \, \pmb{x}+ \pmb{B} \, \pmb{u}. \end{align} \]

Prvý interval činnosti

(6.24)#\[\begin{split} \begin{align} \frac{\mathrm{d} }{\mathrm{d} t} \begin{pmatrix} i_L \\ u_C \end{pmatrix} = % \begin{pmatrix} - \frac{r_L}{L} & 0 \\ 0 & -\frac{1}{R \, C} \end{pmatrix} % \begin{pmatrix} i_{L} \\ u_{C} \end{pmatrix} + % \begin{pmatrix} \frac{1}{L} \end{pmatrix} % \begin{pmatrix} u_{in} \end{pmatrix}. \end{align} \end{split}\]

Druhý interval činnosti

(6.25)#\[\begin{split} \begin{align} \frac{\mathrm{d} }{\mathrm{d} t} \begin{pmatrix} i_L \\ u_C \end{pmatrix} = % \begin{pmatrix} - \frac{r_L}{L} & - \frac{1}{L} \\ \frac{1}{C} & -\frac{1}{R \, C} \end{pmatrix} % \begin{pmatrix} i_{L} \\ u_{C} \end{pmatrix}. \end{align} \end{split}\]

6.3.4. Matlab/Octave#

Ukáž kód

% invertujuci menic
close all
clear all
clc

% parametre obvodu
R = 20;
R2 = 5;
rL = 0.1;
L = 500e-6;
C = 50e-6;

% krok simulacie
dt = 1e-7;
% simulacny cas
Tsim = 30e-3;

% frekvencia spinania
fs=50e3;               

% vstupne napatie
us = 20;
% vystupne napatie
uo = -30;

% pociatocne podmienky
iL=0;
uC=0;
X=[iL;uC];

% pomerna sirka zopnutia
D=uo/(uo-us)

% generovanie piloveho priebehu
t=0:dt:Tsim;
sawt = 0.5+0.5*sawtooth (2*pi*fs*t , 0.5);

n=1;
% nepriama eulerova metoda 
for t=0:dt:Tsim
    % stavove matice
    A1 = [(-rL/L),0;
          0,(-1/(C*R))];
    
    B1 = [(1/L),0; 
          0,0];
    
    A2 = [-(rL/L),(1/L);
      -(1/C),-(1/(C*R))];
    
    B2 = [0,0; 
          0,0];
    % jednotkova matica
    E = eye(size(A1));
    
    % matice nepriamej eulerovej metody
    F1 = inv(E-dt*A1);
    G1 = F1*dt*B1;
    
    F2= inv(E-dt*A2);
    G2= F2*dt*B2;
    
    u = [us;0];
    
    % porovnavanie piloveho priebehu
    % s pomernou sirkou zopnutia
    if(sawt(n) < D)           
        X=F1*X+G1*u;
    else          
        X=F2*X+G2*u; 
    end
    
    iL(n)=X(1);
    uC(n)=X(2);
    
    time(n)=t;
    
    % skokova zmena odporu zataze
    if(time(n) > Tsim/2)
       R=R2;
    end
     
    n=n+1;
end

% priebehy
figure
subplot(2,1,1)
plot(time,iL)
ylabel('iL [A]');
xlabel('t [s]');
grid on

subplot(2,1,2)
plot(time,uC)
ylabel('uC [V]');
xlabel('t [s]');
grid on

Online simulácia

Spustiť simuláciu

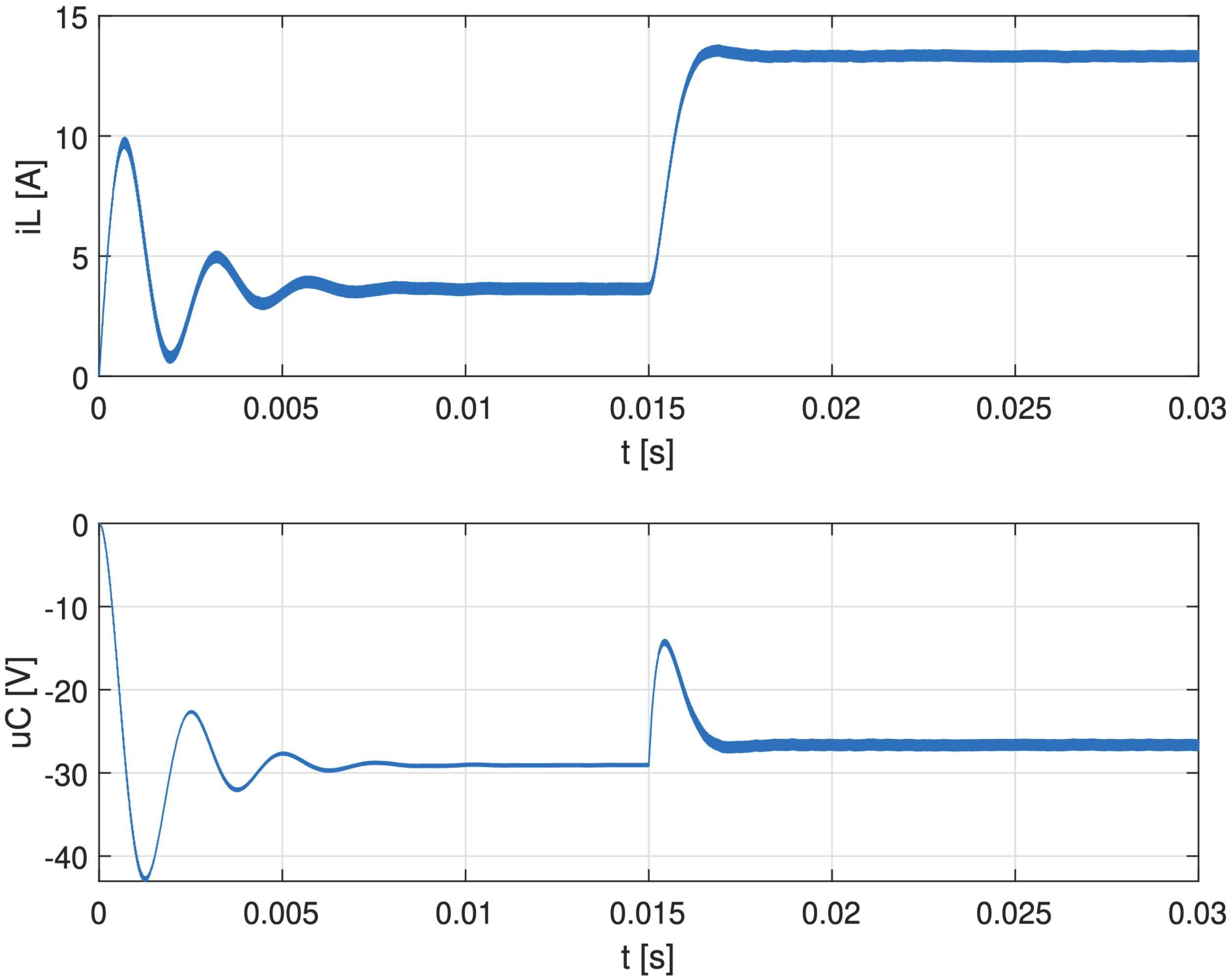
../../../_images/plot_buckboost.png

Obr. 6.20 Priebehy elektrických veličín invertujúceho meniča.#

6.3.5. Zadanie#

Vykonajte analýzu a simuláciu galvanicky neizolovaného invertujúceho meniča typu buck-boost so statickými stratami, Obr. 6.21. Výstupné napätia sú udávané pre ideálny menič.

Parametre simulácie sú \(u_{in} = 15\,\)V, \(u_{out} = -30\) a \(u_{out} = -5\) V, \(R = 20 \,\Omega\), \(L = 500 \,\mu\)H, \(C = 47 \,\mu\)F, \(dt = h = 0.1 \, \mu\)s, \(r_L = 0.5\,\Omega\), \(r_Q = 0.1\,\Omega\), \(r_D = 0.1\,\Omega\), \(r_C = 0.1\,\Omega\), frekvencia spínania \(f = 20\) kHz, skoková zmena záťaže na \(R = 5 \,\Omega\) v čase \(t = 15\) ms, celkový čas simulácie 30 ms.

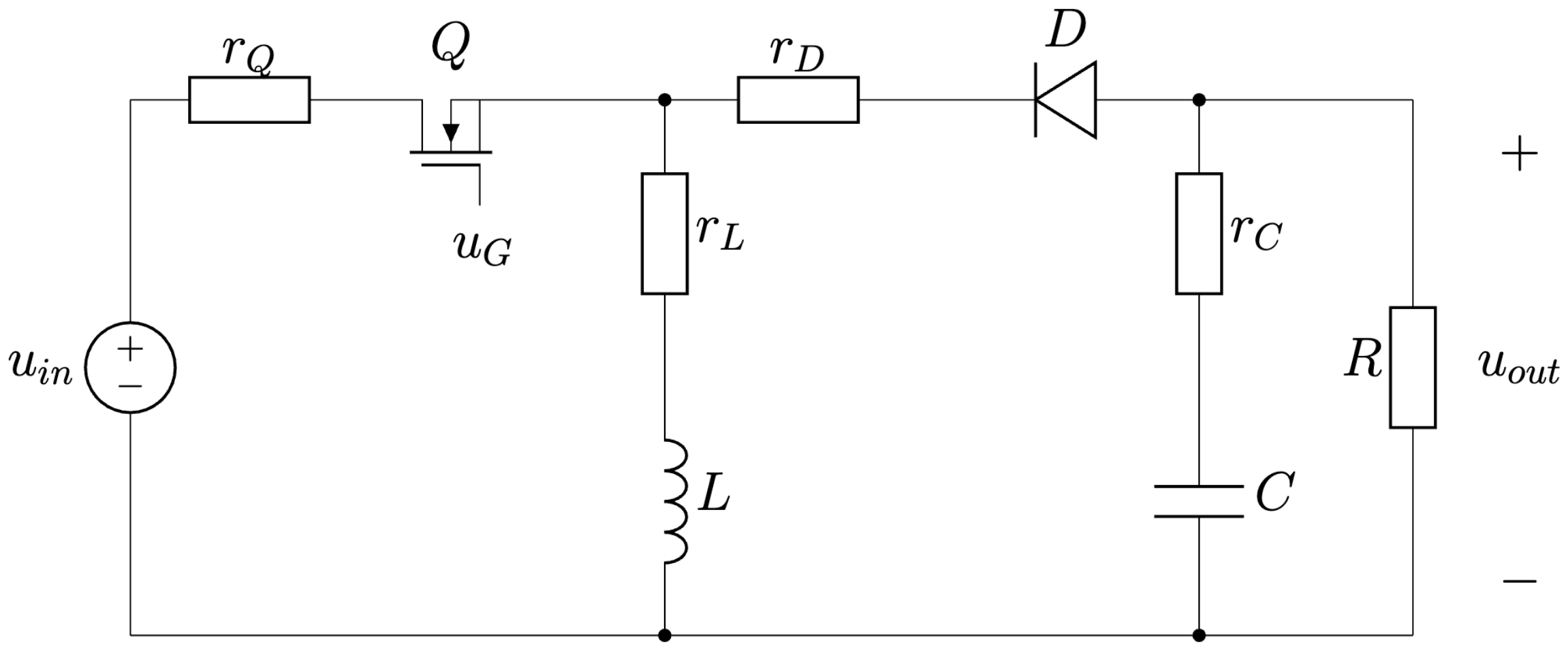
../../../_images/buck_boost_2.png

Obr. 6.21 Invertujúci menič (Buck-Boost) so statickými stratami.#

Postup riešenia: Analyzujte menič, získajte jeho diferenciálne rovnice a jeho zápis v maticovom tvare. Odvoďte hodnotu \(D\) analyticky z prevodových charakteristík ideálnych meničov \(M(D) =u_{out}/u_{in}\) a túto hodnotu používajte pri simulácii. Simulácia meničov pomocou nepriamej Eulerovej metódy v maticovom tvare v prostredí Matlab. Zobrazte priebehy napätí a prúdov všetkých stavových veličín a priebehy napätia a prúdu na záťaži \(R\). Simuláciu vykonajte pre ideálne meniče a meniče so stratami, porovnajte ich výsledky (ideálny/reálny). U meničov, ktoré dokážu napätie zvyšovať aj znižovať, vykonajte simuláciu, zobrazenie priebehov a ich porovnanie, pre dve rôzne hodnoty výstupného napätia podľa zadania. Svoje zistenia a výsledky popíšte v závere.